题目内容
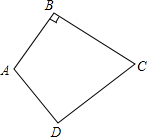 如图,有一张四边形纸片ABCD,AB=AD=6cm,CB=CD=8cm,且∠B=90°.
如图,有一张四边形纸片ABCD,AB=AD=6cm,CB=CD=8cm,且∠B=90°.(1)要把该四边形纸片裁剪成一个面积最大的圆形纸片,你能否用折叠的方法找出圆心?若能,请你度量出圆的半径;
(2)计算出最大圆形纸片的半径.
考点:作图—应用与设计作图
专题:
分析:(1)根据AB=AD=6cm,CB=CD=8cm,且∠B=90°可知△ABC≌ADC,可以折出三个角的对角线,其交点即为圆心;
(2)根据△AOB与△COB的面积之和为△ABC的面积解答.
(2)根据△AOB与△COB的面积之和为△ABC的面积解答.
解答: 解:(1)沿BF折叠,使得BA与BC重合;
解:(1)沿BF折叠,使得BA与BC重合;
连接AC,则AB与AD重合,CB与CD重合;
AC与BM的交点O即为圆心.
测量得半径约为3.5cm.
(2)设⊙O与AB、BC的切点为E、F,
则
AB•EO+
BC•OF=
AB•BC,
即6EO+8FO=6×8,
14FO=48,
FO=
.
 解:(1)沿BF折叠,使得BA与BC重合;
解:(1)沿BF折叠,使得BA与BC重合;连接AC,则AB与AD重合,CB与CD重合;
AC与BM的交点O即为圆心.
测量得半径约为3.5cm.
(2)设⊙O与AB、BC的切点为E、F,
则
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即6EO+8FO=6×8,
14FO=48,
FO=
| 24 |
| 7 |
点评:本题考查了作图--应用与设计作图,要熟悉角平分线的性质及四边形的内切圆.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
已知AB是⊙O的切线,在下列给出的条件中,能判断出AB⊥CD的是( )
| A、AB与⊙O相切于点C |
| B、CD是⊙O的直径 |
| C、AB与⊙O相切于点C,CD是直径 |
| D、CD是⊙O的弦 |

 如图,在正方形ABCD中,取AD,CD的边的中点E,F,连接CE,BF交于点G,连接AG,试判断AG与AB是否相等,并说明理由.
如图,在正方形ABCD中,取AD,CD的边的中点E,F,连接CE,BF交于点G,连接AG,试判断AG与AB是否相等,并说明理由.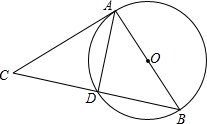 如图,AC切圆O于A,CB顺次交圆O于D、B点,AC=6,DB=5,连接AD、AB.证明:△CAD∽△CBA.
如图,AC切圆O于A,CB顺次交圆O于D、B点,AC=6,DB=5,连接AD、AB.证明:△CAD∽△CBA.