题目内容
已知⊙O的半径等于4cm,AB为⊙O的弦,其长为4
cm,则弦AB所对的圆周角的度数为 .
| 2 |
考点:垂径定理,圆周角定理,解直角三角形
专题:分类讨论
分析:连接OA、OB,∠ACB与∠ADB为弦所对的圆周角作OH⊥AB于H,根据垂径定理得AH=
AB=2
,在Rt△OAH中利用勾股定理计算出OH=2
,于是可判断△OAH为等腰直角三角形,得到∠AOH=45°,则∠AOB=90°,根据圆周角定理得∠ACB=
∠AOB=45°,根据圆内接四边形性质得∠ADB=135°.
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
解答:解:连接OA、OB,∠ACB与∠ADB为弦所对的圆周角,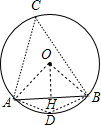 作OH⊥AB于H,
作OH⊥AB于H,
则AH=BH=
AB=2
,
在Rt△OAH中,∵OA=4,AH=2
,
∴OH=
=2
,
∴△OAH为等腰直角三角形,
∴∠AOH=45°,
∴∠AOB=90°,
∴∠ACB=
∠AOB=45°,
∴∠ADB=180°-∠ACB=135°,
即弦AB所对的圆周角的度数为45°或135°.
故答案为45°或135°.
 作OH⊥AB于H,
作OH⊥AB于H,则AH=BH=
| 1 |
| 2 |
| 2 |
在Rt△OAH中,∵OA=4,AH=2
| 2 |
∴OH=
| OA2-AH2 |
| 2 |
∴△OAH为等腰直角三角形,
∴∠AOH=45°,
∴∠AOB=90°,
∴∠ACB=
| 1 |
| 2 |
∴∠ADB=180°-∠ACB=135°,
即弦AB所对的圆周角的度数为45°或135°.
故答案为45°或135°.
点评:本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了圆周角定理.

练习册系列答案
相关题目
李冬坐在教室的第二列第四行,用数对(2,4)来表示,王华坐在第六列第一行,可以用( )来表示.
| A、(1,6) | B、(6,1) |
| C、(0,6) |
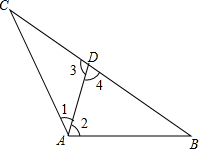 写出如图的符合下列条件的角.(图中所有的角均指小于平角的角).
写出如图的符合下列条件的角.(图中所有的角均指小于平角的角). 如图,AB是⊙O直径,直线DC切⊙O于点C,过点B作BD⊥CD于点D,BD=3,AB=5,求BC.
如图,AB是⊙O直径,直线DC切⊙O于点C,过点B作BD⊥CD于点D,BD=3,AB=5,求BC.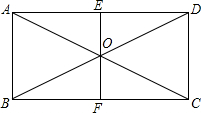 如图,点O为矩形ABCD对角线的交点,过点O作EF⊥BC于点F,若AB=2cm,BC=4cm,求四边形AECF的面积.
如图,点O为矩形ABCD对角线的交点,过点O作EF⊥BC于点F,若AB=2cm,BC=4cm,求四边形AECF的面积.