题目内容
17. 美化城市,改善人居环境,已成为城市建设的一项重要内容,某市近几年通过抓旧房改造、植草、栽树、修建公园等措施,使城区绿化面积不断增大(如图所示).
美化城市,改善人居环境,已成为城市建设的一项重要内容,某市近几年通过抓旧房改造、植草、栽树、修建公园等措施,使城区绿化面积不断增大(如图所示).①根据图表信息填空:2006年底的绿地面积为600000平方米,比2005年底增加了40000平方米,在2004年、2005年、2006年这三年中,绿地面积增加最多的是2005年.
②为满足城市发展的需要,计划在2008年底使城市绿地总面积达72.6公顷,求2007年、2008年这两年绿地面积的年平均增长率.
分析 ①观察统计图可找出2003、2004、2005、2006年底的绿地面积,将每两年的绿地面积做差求出每年的绿地面积增长数,比较后即可得出结论;
②设2007年、2008年这两年绿地面积的年平均增长率为x,根据2008年底城市绿地面积=2006年底城市绿地面积×1加年平均增长率和的平方即可得出关于x的一元二次方程,解之即可得出结论.
解答 解:①60公顷=600000平方米,
60-56=4(公顷)=40000平方米.
∵51-48=3(公顷),56-51=5(公顷),3<4<5,
∴2005年绿地面积增加最多.
故答案为:600000;40000;2005.
②设2007年、2008年这两年绿地面积的年平均增长率为x,
根据题意得:60(1+x)2=72.6,
解得:x=10%或x=-210%(舍去).
答:2007年、2008年这两年绿地面积的年平均增长率为10%.
点评 本题考查了一元二次方程的应用以及折线统计图,解题的关键:①观察折线统计图找出每年的数据;②根据2008年底城市绿地面积=2006年底城市绿地面积×1加年平均增长率和的平方列出关于x的一元二次方程.

练习册系列答案
相关题目
8.某品牌运动服经过两次降价,每件零售价由500元降为315元,已知两次降价的百分率相同,求每次降价的百分率,设每次降价的百分率为x,下面所列的方程中正确的是( )
| A. | 500(1-x)2=315 | B. | 500(1+x)2=315 | C. | 500(1-2x)2=315 | D. | 500(1-x2)=315 |
12.某小组5名同学在一周内参加家务劳动的时间如表所示,关于“劳动时间”的这组数据,以下说法正确的是( )
| 动时间(小时) | 3 | 3.5 | 4 | 4.5 |
| 人数 | 1 | 1 | 2 | 1 |
| A. | 中位数是4,平均数是3.75 | B. | 众数是4,平均数是3.75 | ||
| C. | 中位数是4,平均数是3.8 | D. | 众数是2,平均数是3.8 |
9.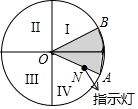 如图所示,将一个圆盘四等分,并把四个区域分别标上Ⅰ、Ⅱ、Ⅲ、Ⅳ,只有区域Ⅰ为感应区域,中心角为55°的扇形AOB绕点0转动,在其半径OA上装有带指示灯的感应装置,当扇形AOB与区域I有重叠(原点除外)的部分时,指示灯会发光,否则不发光,当扇形AOB任意转动时,指示灯发光的概率为( )
如图所示,将一个圆盘四等分,并把四个区域分别标上Ⅰ、Ⅱ、Ⅲ、Ⅳ,只有区域Ⅰ为感应区域,中心角为55°的扇形AOB绕点0转动,在其半径OA上装有带指示灯的感应装置,当扇形AOB与区域I有重叠(原点除外)的部分时,指示灯会发光,否则不发光,当扇形AOB任意转动时,指示灯发光的概率为( )
 如图所示,将一个圆盘四等分,并把四个区域分别标上Ⅰ、Ⅱ、Ⅲ、Ⅳ,只有区域Ⅰ为感应区域,中心角为55°的扇形AOB绕点0转动,在其半径OA上装有带指示灯的感应装置,当扇形AOB与区域I有重叠(原点除外)的部分时,指示灯会发光,否则不发光,当扇形AOB任意转动时,指示灯发光的概率为( )
如图所示,将一个圆盘四等分,并把四个区域分别标上Ⅰ、Ⅱ、Ⅲ、Ⅳ,只有区域Ⅰ为感应区域,中心角为55°的扇形AOB绕点0转动,在其半径OA上装有带指示灯的感应装置,当扇形AOB与区域I有重叠(原点除外)的部分时,指示灯会发光,否则不发光,当扇形AOB任意转动时,指示灯发光的概率为( )| A. | $\frac{1}{6}$ | B. | $\frac{7}{12}$ | C. | $\frac{5}{12}$ | D. | $\frac{5}{9}$ |
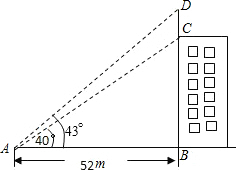 如图,∠BAD=43°,∠BAC=40°,AB=52m,求得避雷针CD的长约4.86m.(结果精确到0.1m)(可用下列参考数据求:sin43°≈0.68,sin40°≈0.64,cos43°≈0.73,cos40°≈0.76,tan43°≈0.93,tan40°≈0.84)
如图,∠BAD=43°,∠BAC=40°,AB=52m,求得避雷针CD的长约4.86m.(结果精确到0.1m)(可用下列参考数据求:sin43°≈0.68,sin40°≈0.64,cos43°≈0.73,cos40°≈0.76,tan43°≈0.93,tan40°≈0.84)