题目内容
△ABC的三个内角∠A、∠B、∠C满足∠A：∠B：∠C=1：2：3，则这个三角形是（ ）
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、任意三角形 |
考点：三角形内角和定理
专题：计算题
分析：根据比例设∠A、∠B、∠C分别为k、2k、3k，然后利用三角形的内角和等于180°列式求出k值，再求出最大的角∠C的度数，即可判断．
解答：解：∵∠A：∠B：∠C=1：2：3，
∴设∠A、∠B、∠C分别为k、2k、3k，
由题意得，k+2k+3k=180°，
解得k=30°，
∠C=3×30°=90°，
∴这个三角形是直角三角形．
故选B．
∴设∠A、∠B、∠C分别为k、2k、3k，
由题意得，k+2k+3k=180°，
解得k=30°，
∠C=3×30°=90°，
∴这个三角形是直角三角形．
故选B．
点评：本题考查了三角形的内角和定理，利用“设k法”求解更加简便．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
2010年4月20日，中央电视台举办“情系玉树，大爱无疆”抗震救灾大型捐款活动．这次活动共募得善款2175000000元人民币．2175000000用科学记数法表示为（ ）
| A、0.2175×109 |
| B、2.175×108 |
| C、2.175×109 |
| D、21.75×108 |
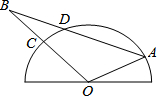如图，半圆O是一个量角器，△AOB为一纸片，AB交半圆于点D，OB交半圆于点C，若点C、D、A在量角器上对应读数分别为45°，70°，160°，则∠B的度数为（ ）| A、20° | B、30° |
| C、45° | D、60° |
若
=
，则
=（ ）
| a |
| b |
| 3 |
| 4 |
| a+b |
| b |
| A、2 | ||
B、
| ||
C、
| ||
D、
|
如图，已知∠B=∠EFD，BF=CE，添加下列一个条件，不能使△ABC≌△DEF的是（ ）| A、∠A=∠D |
| B、∠ACB=∠E |
| C、AB=DF |
| D、AC=DE |
“情系玉树，大爱无疆--抗震救灾大型募捐活动”4月20日晚在中央电视台1号演播大厅举行．据统计，这台募捐晚会共募得善款21.75亿元人民币，约合每秒钟筹集善款16万元．21.75亿元用科学记数法可以表示为（ ）
| A、21.75×108 |
| B、2.175×108 |
| C、21.75×109 |
| D、2.175×109 |
已知△ABC中，∠A=2∠B=3∠C，则△ABC为（ ）
| A、钝角三角形 | B、直角三角形 |
| C、锐角三角形 | D、无法确定 |
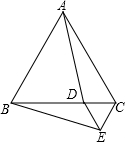如图，△ABC和△DCE都是等边三角形，点D是△ABC的边BC上的一点，连接AD，BE．求证：AD=BE．
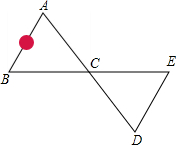如固，为修筑一条公路，需测量出被大石头阻挡的∠BAC的大小，为此，小张师傅便在直线AC上取点D，使AC=CD，在BC的延长线上取点E，使BC=CE，连接DE，只要测出∠D的度数，则可知∠A的度数等于∠D的度数．请说明理由．