题目内容
用计算器计算
,
,
,
…根据你发现的规律,判断P=
与Q=
(n>1且n为整数)的值的大小关系.
|
|
|
|
|
|
考点:计算器—数的开方
专题:规律型
分析:把被开方数的分子分解因式,然后约分表示出P、Q,再判断出大小关系即可.
解答:解:∵
=
=n+1,
=
=(n+1)+1=n+2,
∴P=
,Q=
,
∵n>1且n为整数,n+2>n+1,
∴P<Q.
| n2-1 |
| n-1 |
| (n+1)(n-1) |
| n-1 |
| (n+1)2-1 |
| (n+1)-1 |
| [(n+1)+1][(n+1)-1] |
| (n+1)-1 |
∴P=
| n+1 |
| n+2 |
∵n>1且n为整数,n+2>n+1,
∴P<Q.
点评:本题考查了二次根式的除法,把被开方数分解因式表示出P、Q是解题的关键.

练习册系列答案
相关题目
下列命题中真命题是( )
①内错角相等;
②如果a+b=0,那么
=
;
③邻补角互补;
④相等的角是对顶角;
⑤如果a+b=0,那么
=
.
①内错角相等;
②如果a+b=0,那么
| 3 | a |
| 3 | -b |
③邻补角互补;
④相等的角是对顶角;
⑤如果a+b=0,那么
| a2 |
| b2 |
| A、①②③④⑤ | B、②③④⑤ |
| C、②③⑤ | D、①④⑤ |
 如图,已知∠B=∠EFD,BF=CE,添加下列一个条件,不能使△ABC≌△DEF的是( )
如图,已知∠B=∠EFD,BF=CE,添加下列一个条件,不能使△ABC≌△DEF的是( )| A、∠A=∠D |
| B、∠ACB=∠E |
| C、AB=DF |
| D、AC=DE |
已知△ABC中,∠A=2∠B=3∠C,则△ABC为( )
| A、钝角三角形 | B、直角三角形 |
| C、锐角三角形 | D、无法确定 |
 如图,已知BD,CE分别是△ABC的外角平分线,过点A分别作BD,CE的垂线,交BD,CE于点F,G,交直线BC于点M,N.求证:FG∥MN,FG=
如图,已知BD,CE分别是△ABC的外角平分线,过点A分别作BD,CE的垂线,交BD,CE于点F,G,交直线BC于点M,N.求证:FG∥MN,FG=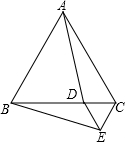 如图,△ABC和△DCE都是等边三角形,点D是△ABC的边BC上的一点,连接AD,BE.求证:AD=BE.
如图,△ABC和△DCE都是等边三角形,点D是△ABC的边BC上的一点,连接AD,BE.求证:AD=BE. 如图,在7×8的方格纸中,已知图中每个小正方形的边长都为1,求图中阴影部分的面积.
如图,在7×8的方格纸中,已知图中每个小正方形的边长都为1,求图中阴影部分的面积. 如图,等腰梯形ABCD是一个四棱柱的俯视图,它的高为5,AD=3,AE⊥BC于点E,AE=4,BC=7,求此四棱柱的三种视图的面积和.
如图,等腰梯形ABCD是一个四棱柱的俯视图,它的高为5,AD=3,AE⊥BC于点E,AE=4,BC=7,求此四棱柱的三种视图的面积和.