题目内容
若n是整数,证明(2n+1)2-(2n-1)2是8的倍数.
考点:因式分解-运用公式法
专题:计算题
分析:原式利用平方差公式分解,即可得到结果为8的倍数.
解答:证明:(2n+1)2-(2n-1)2=[(2n+1)+(2n-1)][(2n+1)-(2n-1)]=4n×2=8n,
∵n为整数,
∴结果为8的倍数.
答:(2n+1)2-(2n-1)2是8的倍数.
∵n为整数,
∴结果为8的倍数.
答:(2n+1)2-(2n-1)2是8的倍数.
点评:此题考查了因式分解-运用公式法,熟练掌握公式是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
Rt△ABC中,∠C=90°,AB=3,则AB2+AC2+BC2=( )
| A、6 | B、8 | C、16 | D、18 |
若
=
,则
=( )
| a |
| b |
| 3 |
| 4 |
| a+b |
| b |
| A、2 | ||
B、
| ||
C、
| ||
D、
|
“情系玉树,大爱无疆--抗震救灾大型募捐活动”4月20日晚在中央电视台1号演播大厅举行.据统计,这台募捐晚会共募得善款21.75亿元人民币,约合每秒钟筹集善款16万元.21.75亿元用科学记数法可以表示为( )
| A、21.75×108 |
| B、2.175×108 |
| C、21.75×109 |
| D、2.175×109 |
已知△ABC中,∠A=2∠B=3∠C,则△ABC为( )
| A、钝角三角形 | B、直角三角形 |
| C、锐角三角形 | D、无法确定 |
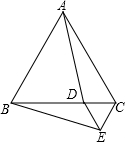 如图,△ABC和△DCE都是等边三角形,点D是△ABC的边BC上的一点,连接AD,BE.求证:AD=BE.
如图,△ABC和△DCE都是等边三角形,点D是△ABC的边BC上的一点,连接AD,BE.求证:AD=BE. 如图,在矩形ABCD中,M是BC的中点,MA⊥MD.若矩形的周长为48cm,求矩形的面积.
如图,在矩形ABCD中,M是BC的中点,MA⊥MD.若矩形的周长为48cm,求矩形的面积.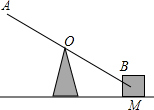 如图,某人在A处利用杠杆抬起位于B处的重物M.已知重物M的质量为50kg,杠杆与地面的夹角为30°,在A处的人和B处的重物与支架的顶端O的水平距离都为3m.试问:该人将重物M抬至水平位置所做的功是多少焦耳(精确到0.1,
如图,某人在A处利用杠杆抬起位于B处的重物M.已知重物M的质量为50kg,杠杆与地面的夹角为30°,在A处的人和B处的重物与支架的顶端O的水平距离都为3m.试问:该人将重物M抬至水平位置所做的功是多少焦耳(精确到0.1,