题目内容
6.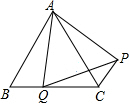 如图,点Q是等边△ABC的边BC上一点,以AQ为边作等边△AQP,求证:PC∥AB.
如图,点Q是等边△ABC的边BC上一点,以AQ为边作等边△AQP,求证:PC∥AB.
分析 延长PC到点D,使CD=BQ,如图,BC=QD,根据等边三角形的性质得∠B=60°,AB=BC,AQ=QP,∠AQP=60°,再利用三角形外角性质可证明∠1=∠2,于是可根据“SAS”判定△ABQ≌△QDP,得到BQ=DP,∠B=∠D=60°,所以DC=DP,则可判断△DCP为等边三角形得到∠PCD=60°,然后根据平行线的性质得到PC∥AB.
解答 证明:延长PC到点D,使CD=BQ,如图,BC=QD,
∵△ABC为等边三角形,
∴∠B=60°,AB=BC,
∴AB=QD,
∵△APQ为等边三角形,
∴AQ=QP,∠AQP=60°,
∵∠AQD=∠1+∠B,即∠2+AQP=∠1+B,
∴∠1=∠2,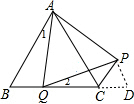
在△ABQ和△QDP中,
$\left\{\begin{array}{l}{AB=QD}\\{∠1=∠2}\\{AQ=QP}\end{array}\right.$,
∴△ABQ≌△QDP,
∴BQ=DP,∠B=∠D=60°,
∴DC=DP,
∴△DCP为等边三角形,
∴∠PCD=60°,
∴∠PCD=∠B,
∴PC∥AB.
点评 本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.也考查了等边三角形的判定与性质.构造△QPD与△ABQ全等是解决此题的关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
15.下列各组线段能构成直角三角形的一组是( )
| A. | 5cm,9cm,12cm | B. | 7cm,12cm,13cm | C. | 30cm,40cm,50cm | D. | 3cm,4cm,6cm |
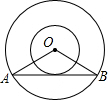 如图,⊙O的半径为8cm,圆内的弦AB=8$\sqrt{3}cm$,以点O为圆心,4cm为半径作小圆,求证:直线AB与小圆相切.
如图,⊙O的半径为8cm,圆内的弦AB=8$\sqrt{3}cm$,以点O为圆心,4cm为半径作小圆,求证:直线AB与小圆相切.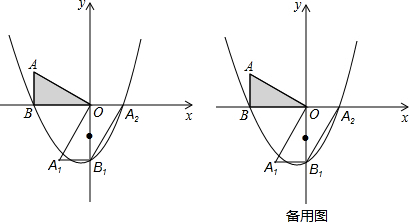
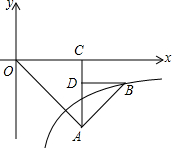 如图,△OAC和△BAD都是等腰直角三角形,反比例函数在第四象限经过点B,若OA2-AB2=8,则k的值为-4.
如图,△OAC和△BAD都是等腰直角三角形,反比例函数在第四象限经过点B,若OA2-AB2=8,则k的值为-4.