题目内容
20. 如图,已知抛物线y=ax2-$\frac{3}{2}$x+c与x轴相交于A、B两点,与y轴相交于C点,已知点A、B的坐标分别是A(-1,0)、B(4,0).
如图,已知抛物线y=ax2-$\frac{3}{2}$x+c与x轴相交于A、B两点,与y轴相交于C点,已知点A、B的坐标分别是A(-1,0)、B(4,0).(1)求该抛物线的解析式;
(2)在x轴上是否存在一点P,使△PBC是以BC为腰的等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
分析 (1)由于已知抛物线与x轴的交点,则可设交点式y=a(x+1)(x-4),化为一般式得到y=ax2-3ax-4a,则-3a=-$\frac{3}{2}$,然后求出a的值即可得到抛物线解析式;
(2)先求出C点坐标,再计算出BC的长,然后分类讨论:分别以点B、C为圆心,BC为半径画弧,弧与x轴的交点即为P点,然后写出对应的P点坐标.
解答  解:(1)设抛物线的解析式为y=a(x+1)(x-4),
解:(1)设抛物线的解析式为y=a(x+1)(x-4),
即y=ax2-3ax-4a,
所以-3a=-$\frac{3}{2}$,解得a=$\frac{1}{2}$,
所以抛物线解析式为y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2;
(2)存在.
当x=0时,y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2=-2,则C(0,-2),
所以BC=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
当CP=CB时,点P与点B关于y轴对称,此时P点坐标为(-4,0);
当BP=BC=2$\sqrt{5}$时,若点P在B点左侧,P点坐标为(-2$\sqrt{5}$+4,0),若点P在B点右侧,P点坐标为(2$\sqrt{5}$+4,0),
综上所述,满足条件的P点坐标为(-4,0)或(-2$\sqrt{5}$+4,0)或(2$\sqrt{5}$+4,0).
点评 本题考查了抛物线与x轴的交点:从二次函数的交点式:y=a(x-x1)(x-x2)(a,b,c是常数,a≠0)中可直接得到抛物线与x轴的交点坐标(x1,0),(x2,0).解决(2)小问的关键是应用分类讨论的思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.某市规定如下用水收费标准:每户每月用水不超过6立方米时,水费按每立方米a元收费;超过6立方米时,不超过的部分每立方米仍按a元收费,超过的部分每立方米按b元收费.该市某户今年3、4月份的用水量和水费如下表所示:
(1)求出a与b的值;
(2)求当用户用水为x立方米时的水费(用含x的代数式表示);
(3)某用户某月交水费39元,这个月该用户用水多少立方米?
| 月份 | 用水量(立方米) | 水费(元) |
| 3 | 5 | 7.5 |
| 4 | 9 | 27 |
(2)求当用户用水为x立方米时的水费(用含x的代数式表示);
(3)某用户某月交水费39元,这个月该用户用水多少立方米?
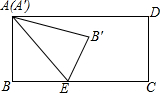 如图,矩形ABCD的边AB=4,BC=7,E为BC上一点,BE=3,连接AE,将矩形ABCD沿AE翻折,翻折后点B与点B′对应,点A与A′对应,再将所得△A′B′E绕着点E旋转,线段A′B′与线段AE交于点P,当PA′=2.4时,△B′AP为等腰三角形.
如图,矩形ABCD的边AB=4,BC=7,E为BC上一点,BE=3,连接AE,将矩形ABCD沿AE翻折,翻折后点B与点B′对应,点A与A′对应,再将所得△A′B′E绕着点E旋转,线段A′B′与线段AE交于点P,当PA′=2.4时,△B′AP为等腰三角形. 如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了8步路(假设2步为1米),却踩伤了花草.
如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了8步路(假设2步为1米),却踩伤了花草.