题目内容
10.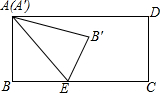 如图,矩形ABCD的边AB=4,BC=7,E为BC上一点,BE=3,连接AE,将矩形ABCD沿AE翻折,翻折后点B与点B′对应,点A与A′对应,再将所得△A′B′E绕着点E旋转,线段A′B′与线段AE交于点P,当PA′=2.4时,△B′AP为等腰三角形.
如图,矩形ABCD的边AB=4,BC=7,E为BC上一点,BE=3,连接AE,将矩形ABCD沿AE翻折,翻折后点B与点B′对应,点A与A′对应,再将所得△A′B′E绕着点E旋转,线段A′B′与线段AE交于点P,当PA′=2.4时,△B′AP为等腰三角形.
分析 根据勾股定理求得AE,根据等腰三角形的性质得出PA=PB′,设PA=PB′=x,则PA′=4-x,PE=5-x,作PG⊥A′E于G,根据余弦函数求得A′G=$\frac{4}{5}$(4-x),进而得出GE=5-$\frac{4}{5}$(4-x),然后根据勾股定理列出关于x的方程,解方程即可求得.
解答 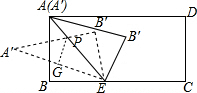 解:∵AB=4,BE=3,
解:∵AB=4,BE=3,
∴AE=5,
∵△B′AP为等腰三角形,
∴PA=PB′,
设PA=PB′=x,则PA′=4-x,PE=5-x,
作PG⊥A′E于G,
∵∠PA′G=∠BAE,
∴cos∠PA′G=cos∠BAE,
∴$\frac{A′G}{PA′}$=$\frac{AB}{AE}$=$\frac{4}{5}$,
∴A′G=$\frac{4}{5}$(4-x),
∵A′E=AE=5,
∴GE=5-$\frac{4}{5}$(4-x),
∵PA′2-A′G2=PE2-GE2,
∴(4-x)2-[$\frac{4}{5}$(4-x)]2=(5-x)2-[5-$\frac{4}{5}$(4-x)]2
解得x=2.4,
故当PA′=2.4时,△B′AP为等腰三角形.
故答案为2.4.
点评 考查了等腰三角形的性质、勾股定理和旋转的性质,根据勾股定理列出方程是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
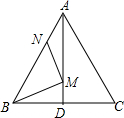 如图,在等边△ABC中,AB=4,N为线段AB上的任意一点,∠BAC的平分线交BC于点D,M是AD上的动点,连结BM、MN,则BM+MN的最小值是2$\sqrt{3}$.
如图,在等边△ABC中,AB=4,N为线段AB上的任意一点,∠BAC的平分线交BC于点D,M是AD上的动点,连结BM、MN,则BM+MN的最小值是2$\sqrt{3}$. 如图,在等腰△ABC中,AB=AC,∠A=40°,BD⊥AC于点D,则∠CBD=20°.
如图,在等腰△ABC中,AB=AC,∠A=40°,BD⊥AC于点D,则∠CBD=20°. 如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2).用一条长为a个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D-A-B…的规律紧绕在四边形ABCD的边上.
如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2).用一条长为a个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D-A-B…的规律紧绕在四边形ABCD的边上. 如图,已知抛物线y=ax2-$\frac{3}{2}$x+c与x轴相交于A、B两点,与y轴相交于C点,已知点A、B的坐标分别是A(-1,0)、B(4,0).
如图,已知抛物线y=ax2-$\frac{3}{2}$x+c与x轴相交于A、B两点,与y轴相交于C点,已知点A、B的坐标分别是A(-1,0)、B(4,0).