题目内容
2.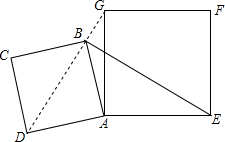 已知:正方形ABCD和正方形AEFG,AD=2,AE=2$\sqrt{2}$,将正方形ABCD绕点A逆时针旋转,如图,当G恰好落在线段DB的延长线上时,则BE的长=$\sqrt{2}$+$\sqrt{6}$.
已知:正方形ABCD和正方形AEFG,AD=2,AE=2$\sqrt{2}$,将正方形ABCD绕点A逆时针旋转,如图,当G恰好落在线段DB的延长线上时,则BE的长=$\sqrt{2}$+$\sqrt{6}$.
分析 作AH⊥DG于H,如图,先根据正方形的性质判断△AHD为等腰直角三角形,则HD=HA=$\frac{\sqrt{2}}{2}$AD=$\sqrt{2}$,再在Rt△AHG中利用勾股定理计算出GH=$\sqrt{6}$,则BG=DH+HG=$\sqrt{2}$+$\sqrt{6}$,由于∠DAB=90°,∠EAG=90°,AD=AB,AG=AE,于是根据旋转的定义可把△ADG绕点A顺时针旋转90°得到△ABE,然后根据旋转的性质即可得到DG=BE=$\sqrt{2}$+$\sqrt{6}$.
解答 解:作AH⊥DG于H,如图,
∵BD为正方形ABCD的对角线,
∴△AHD为等腰直角三角形,
∴HD=HA=$\frac{\sqrt{2}}{2}$AD=$\frac{\sqrt{2}}{2}$×2=$\sqrt{2}$,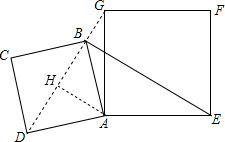
∵四边形AEFG为正方形,
∴AG=AE=2$\sqrt{2}$,
在Rt△AHG中,GH=$\sqrt{A{G}^{2}-A{H}^{2}}$=$\sqrt{(2\sqrt{2})^{2}-(\sqrt{2})^{2}}$=$\sqrt{6}$,
∴BG=DH+HG=$\sqrt{2}$+$\sqrt{6}$,
∵四边形ABCD和四边形AEFG为正方形,
∴∠DAB=90°,∠EAG=90°,AD=AB,AG=AE,
∴△ADG绕点A顺时针旋转90°可得到△ABE,
∴DG=BE=$\sqrt{2}$+$\sqrt{6}$.
故答案为$\sqrt{2}$+$\sqrt{6}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.本题的关键是DG=BE.

练习册系列答案
相关题目
14.作图题:
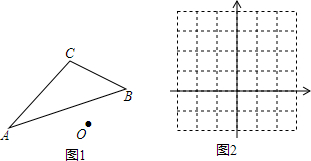
(1)请在图1中作出△ABC关于点O对称的△A′B′C′(不写作法,但要保留作图痕迹)
(2)画二次函数y=$\frac{1}{2}$x2的图象.
解:①列表如下(补充完成下表)
②描点(请在图中描出上表中的点)
③连线(在图中连线,画出y=$\frac{1}{2}$x2的图象)即为所求.

(1)请在图1中作出△ABC关于点O对称的△A′B′C′(不写作法,但要保留作图痕迹)
(2)画二次函数y=$\frac{1}{2}$x2的图象.
解:①列表如下(补充完成下表)
| x | … | -2 | -1 | 0 | 1 | … | |
| y | … | 0.5 | 0 | 0.5 | 2 | … |
③连线(在图中连线,画出y=$\frac{1}{2}$x2的图象)即为所求.
11.下列运算正确的是( )
| A. | (-3)+5=-2 | B. | (-$\frac{1}{3}$)÷(-3)=1 | C. | (-3)×(-4)×(-5)=60 | D. | (-6)+(-3)=-9 |
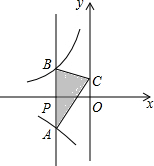 如图,过x轴负半轴上的任意一点P,作y轴的平行线,分别与反比例函数y=$\frac{-6}{x}$,y=$\frac{4}{x}$交于A,B两点.若点C是y轴上任意一点,连接AC,BC,则△ABC的面积是5.
如图,过x轴负半轴上的任意一点P,作y轴的平行线,分别与反比例函数y=$\frac{-6}{x}$,y=$\frac{4}{x}$交于A,B两点.若点C是y轴上任意一点,连接AC,BC,则△ABC的面积是5. 解下列不等式,并把解集在数轴上表示出来.
解下列不等式,并把解集在数轴上表示出来.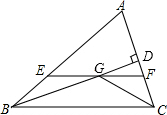 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点G,过点G作EF∥BC交AB于E,交AC于F,过点G作GD⊥AC于D,下列四个结论:
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点G,过点G作EF∥BC交AB于E,交AC于F,过点G作GD⊥AC于D,下列四个结论: