题目内容
3.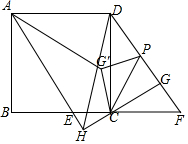 如图,正方形ABCD中,点E在BC边上,连接AE,过AD作DF∥AE交BC的延长线于点F,过点C作CG⊥DF于点G.延长AE、GC交于点H,点P是线段DG上的一点,连接CP,将△CPG沿CP翻折得到△CPG′,连接AG′,若CH=1,DH=3$\sqrt{2}$,则AG′长度的最小值是$\sqrt{26}$-2.
如图,正方形ABCD中,点E在BC边上,连接AE,过AD作DF∥AE交BC的延长线于点F,过点C作CG⊥DF于点G.延长AE、GC交于点H,点P是线段DG上的一点,连接CP,将△CPG沿CP翻折得到△CPG′,连接AG′,若CH=1,DH=3$\sqrt{2}$,则AG′长度的最小值是$\sqrt{26}$-2.
分析 如图,作DM⊥AE于M,首先证明四边形DMHG是正方形,求出正方形DMHG的边长,以及AC的长,因为点P在线段DG上运动时,点G′在以C为圆心,CG为半径的圆上运动,所以当A、G′、C共线时,AG′最小.由此即可解决问题.
解答 解:如图,作DM⊥AE于M.
∵AH∥DF,GH⊥DF,
∴∠MHG=∠HGD=∠DMH=90°,
∴四边形DMHG是矩形,
∵∠ADC=∠MDG=90°,
∴∠ADM=∠CDG,
在△ADM和△CDG中,
$\left\{\begin{array}{l}{∠AMD=∠DGC}\\{∠ADM=∠CDG}\\{AD=DC}\end{array}\right.$,
∴△ADM≌△CDG(AAS),
∴DM=DG,
∴四边形DMHG是正方形,
∵DH=3$\sqrt{2}$,
∴DM=MH=GH=DG=3,
∵CH=1,
∴CG=HG-HC=2,
在Rt△DCG中,CD=$\sqrt{D{G}^{2}+C{G}^{2}}$=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$,
∴AC=$\sqrt{2}$CD=$\sqrt{26}$,
∵点P在线段DG上运动时,点G′在以C为圆心,CG为半径的圆上运动,
∴当A、G′、C共线时,AG′最小,
∴AG′的最小值为AC-CG′=$\sqrt{26}$-2.
故答案为$\sqrt{26}$-2.
点评 本题考查翻折变换、正方形的判定和性质、勾股定理、全等三角形的判定和性质、圆的有关知识,解题的关键是学会常用辅助线的作法,构造全等三角形解决问题,学会求圆外一点到圆上的点的距离的最大值以及最小值,属于中考填空题中的压轴题.

练习册系列答案
相关题目
12.关于二次函数y=-2x2+1,下列说法错误的是( )
| A. | 图象开口向下 | B. | 图象的对称轴为x=$\frac{1}{2}$ | ||
| C. | 函数最大值为1 | D. | 当x>1时,y随x的增大而减小 |
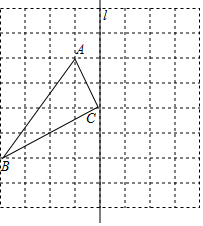 如图,在8×8的正方形网格中,每个小正方形的边长都是1,已知△ABC的三个顶点在格点上.
如图,在8×8的正方形网格中,每个小正方形的边长都是1,已知△ABC的三个顶点在格点上.