题目内容
1.如图,在Rt△ABC中,∠C=90°,AC=BC=4cm,点D为AC边上一点,且AD=3cm,动点E从点A出发沿线段AB向终点B运动.作∠DEF=45°,与边BC相交于点F.(1)找出图中的一对相似三角形,并说明理由;
(2)当△BEF为等腰三角形时,求AE的长;
(3)求动点E从点A出发沿线段AB向终点B运动的过程中点F的运动路线长.

分析 (1)由等腰直角三角形的性质得出∠A=∠B=45°由三角形的外角性质和已知条件证出∠ADE=∠BEF,即可得出结论;
(2)分三种情况:①若EF=BF,由相似三角形的性质和勾股定理求出AE=DE=$\frac{3}{2}\sqrt{2}$即可;
②若EF=BE,由相似三角形的性质和勾股定理求出AE即可;
③若BF=BE,则∠FEB=∠EFB,由△ADE∽△BEF得出AE=AD=3即可.
(3)由(1)得出△ADE∽△BEF,得到$\frac{AD}{BE}$=$\frac{AE}{BF}$,得出y是x的二次函数,即可得出结果.
解答 解:(1)△ADE∽△BEF,理由如下:
∵在Rt△ABC中,∠C=90°,AC=BC=4cm,
∴∠A=∠B=45°,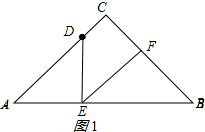
∵∠DEB=∠A+∠ADE=∠DEF+∠BEF,∠DEF=45°,
∴∠ADE=∠BEF,
∴△ADE∽△BEF;
(2)分三种情况
①如图1,若EF=BF,则∠B=∠BEF,
又∵△ADE∽△BEF,
∴∠A=∠ADE=45°,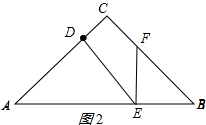
∴∠AED=90°,
∴AE=DE=$\frac{3}{2}\sqrt{2}$;
②如图2,若EF=BE,则∠B=∠EFB
又∵△ADE∽△BEF,
∴∠A=∠AED=45°,
∴∠ADE=90°,
∴AE=3$\sqrt{2}$;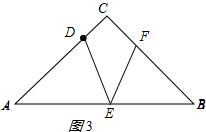
③如图3,若BF=BE,则∠FEB=∠EFB
又∵△ADE∽△BEF,
∴∠ADE=∠AED,
∴AE=AD=3.
综上所述,当△BEF为等腰三角形时,AE的长为$\frac{3}{2}\sqrt{2}$或3$\sqrt{2}$或3.
(3)设AE=xcm,BF长为ycm.
∵在△ABC中,∠C=90°,AC=BC=4.
∴∠A=∠B=45°,AB=4$\sqrt{2}$,
由(1)得:△ADE∽△BEF,
∴$\frac{AD}{BE}$=$\frac{AE}{BF}$,
∴$\frac{3}{4\sqrt{2}-x}$=$\frac{x}{y}$
∴y=-$\frac{1}{3}$x2+$\frac{4}{3}\sqrt{2}$x,
∴y=-$\frac{1}{3}$x2+$\frac{4}{3}\sqrt{2}$x=-$\frac{1}{3}$(x-2$\sqrt{2}$)2+$\frac{8}{3}$,
∴当x=2$\sqrt{2}$时,y有最大值=$\frac{8}{3}$,
当E到达AB中点时,F距离B最远;当E越过A运动,最终和B重合(严格说无限接近B),
∴F的路线是一来一回,即BF的最大值的2倍,
∴点F运动路程为2×$\frac{8}{3}$cm=$\frac{16}{3}$cm.
点评 本题主要考查了二次函数的最值,相似三角形的性质和判定,勾股定理,等腰三角形的性质等知识点的理解和掌握,灵活运用性质进行计算是解此题的关键,用的数学思想是分类讨论思想.

| A. | $\sqrt{12}$是有理数 | B. | 面积为12的正方形边长是$\sqrt{12}$ | ||
| C. | $\sqrt{12}$=2$\sqrt{3}$ | D. | 在数轴上可以找到表示$\sqrt{12}$的点 |
 从△ABC(CB<CA)中裁出一个以AB为底边的等腰△ABD,并使得△ABD的面积尽可能大.
从△ABC(CB<CA)中裁出一个以AB为底边的等腰△ABD,并使得△ABD的面积尽可能大.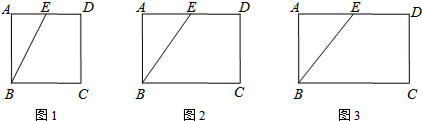
 如图,矩形ABCD是供一辆机动车停放的车位示意图,已知BC=2m,CD=5.4m,∠DCF=30°,请你计算车位所占的宽度EF约为多少米.(结果精确到0.1m,$\sqrt{3}$≈1.73)
如图,矩形ABCD是供一辆机动车停放的车位示意图,已知BC=2m,CD=5.4m,∠DCF=30°,请你计算车位所占的宽度EF约为多少米.(结果精确到0.1m,$\sqrt{3}$≈1.73) 在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.