题目内容
12．下列有理式中①$\frac{2}{x}$，②$\frac{x+y}{5}$，③$\frac{1}{2-a}$，④$\frac{x}{2}$中分式有（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
分析 判断分式的依据是看分母中是否含有字母，如果含有字母则是分式，如果不含有字母则不是分式．
解答 解：①$\frac{2}{x}$，③$\frac{1}{2-a}$的分母中含有字母，属于分式．
②$\frac{x+y}{5}$，④$\frac{x}{2}$的分母中不含有字母，不属于分式．
故选：B．
点评 本题考查的是分式的定义，在解答此题时要注意分式是形式定义，只要是分母中含有未知数的式子即为分式．
练习册系列答案
应用题作业本系列答案
相关题目
小明和小刚用如图所示的两个均匀的转盘做配紫色游戏，游戏规则是：分别任意旋转两个转盘，若其中一个转盘转出了红色，另一个转出了蓝色，则可以配成紫色．若配成紫色则小刚获胜，否则小明获胜．
3．
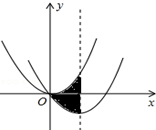如图，在平面直角坐标系中，抛物线y=$\frac{1}{3}$x2经过平移得到抛物线y=ax2+bx，其对称轴与两段抛物线所围成的阴影部分的面积为$\frac{8}{3}$，则a、b的值分别为（ ）
如图，在平面直角坐标系中，抛物线y=$\frac{1}{3}$x2经过平移得到抛物线y=ax2+bx，其对称轴与两段抛物线所围成的阴影部分的面积为$\frac{8}{3}$，则a、b的值分别为（ ）| A． | $\frac{1}{3}$，$\frac{4}{3}$ | B． | $\frac{1}{3}$，-$\frac{8}{3}$ | C． | $\frac{1}{3}$，-$\frac{4}{3}$ | D． | -$\frac{1}{3}$，$\frac{4}{3}$ |
20．函数$y=\frac{{\sqrt{x+2}}}{x-4}$中，自变量x的取值范围是（ ）
| A． | x＞4 | B． | x≥-2且x≠4 | C． | x＞-2且x≠4 | D． | x≠4 |
17．下列二次根式中的最简二次根式是（ ）
| A． | $\sqrt{8}$ | B． | $\sqrt{12}$ | C． | $\sqrt{\frac{1}{2}}$ | D． | $\sqrt{30}$ |
