Question

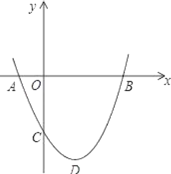
【题目】在平面直角坐标系中，点O为坐标原点，抛物线y=ax2+bx+c与x轴交于点A（-1，0），B（3，0），与y轴交于点C（0，3），顶点为G．

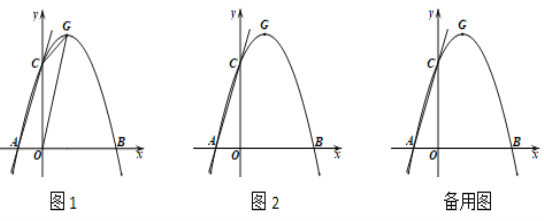
（1）求抛物线和直线AC的解析式；

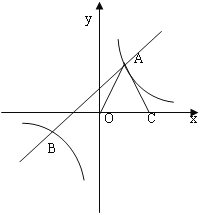
（2）如图1，设E（m，0）为x正半轴上的一个动点，若△CGE和△CGO的面积满足S△CGE=S△CGO，求点E的坐标；

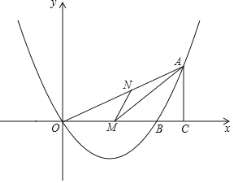
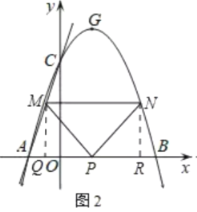
（3）如图2，设点P从点A出发，以每秒1个单位长度的速度沿x轴向右运动，运动时间为ts，点M为射线AC上一动点，过点M作MN∥x轴交抛物线对称轴右侧部分于点N．试探究点P在运动过程中，是否存在以P，M，N为顶点的三角形为等腰直角三角形，若存在，求出t的值；若不存在，请说明理由．

Answer 1

【答案】（1）；y=3x+3；（2）点E的坐标为：（1,0）或（-7,0）；（3）存在，t的值为或或．

【解析】

（1）用待定系数法即能求出抛物线和直线AC解析式．
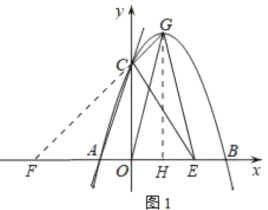
（2）△CGE与△CGO虽然有公共底边CG，但高不好求，故把△CGE构造在比较好求的三角形内计算．延长GC交x轴于点F，则△FGE与△FCE的差即为△CGE．
（3）设M的坐标（e，3e＋3），分别以M、N、P为直角顶点作分类讨论，利用等腰直角三角形的特殊线段长度关系，用e表示相关线段并列方程求解，再根据e与AP的关系求t的值．

解：（1）将点A（-1，0），B（3，0），点C（0，3）代入抛物线y=ax2+bx+c得，

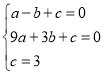，解得，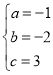

∴，

设直线AC的解析式为y=kx+n，

将点A（-1，0），点C（0，3）代入得：，解得：k=3，n=3

∴直线AC的解析式为：y=3x+3

（2）延长GC交x轴于点F，过点G作GH⊥x轴于点H，

∵

∴G（1,4），GH=4，

∴，

若S△CGE=S△CGO，

则S△CGE=S△CGO=，

①若点E在x轴的正半轴，

设直线CG为，将G（1,4）代入得

∴，

∴直线CG的解析式为y=x+3，

∴当y=0时，x=-3，即F(-3,0)

∵E（m,0）

∴EF=m-(-3)=m+3

∴

=

=

=

=

∴，解得：m=1

∴E的坐标为（1,0）

②若点E在x轴的负半轴上，则点E到直线CG的距离与点（1,0）到直线CG的距离相等，

即点E到点F的距离等于点（1,0）到点F的距离，

∴EF=-3-m=1-(-3)=4

∴m=-7，即E（-7,0）

综上所述，点E的坐标为：（1,0）或（-7,0）

（3）存在以P，M，N为顶点的三角形为等腰直角三角形，

设M（e,3e+3），e＞-1，则，

①如图2，若∠MPN=90°，PM=PN，

过点M作MQ⊥x轴于点Q，过N作NR⊥x轴于点R，

∵MN∥x轴
∴MQ＝NR＝3e＋3
∴Rt△MQP≌Rt△NRP（HL）
∴PQ＝PR，∠MPQ＝∠NPR＝45°
∴MQ＝PQ＝PR＝NR＝3e＋3
∴xN＝xM＋3e＋3＋3e＋3＝7e＋6，即N（7e＋6，3e＋3）
∵N在抛物线上
∴（7e＋6）2＋2（7e＋6）＋3＝3e＋3，

解得：（舍去），

∵AP＝t，OP＝t1，OP＋OQ＝PQ
∴t1e＝3e＋3
∴t＝4e＋4＝，

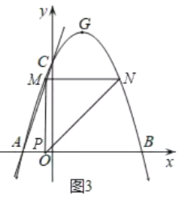
②如图3，若∠PMN＝90°，PM＝MN，

∴MN＝PM＝3e＋3
∴xN＝xM＋3e＋3＝4e＋3，即N（4e＋3，3e＋3）
∴（4e＋3）2＋2（4e＋3）＋3＝3e＋3
解得：e1＝1（舍去），e2＝，
∴t＝AP＝e（1）＝，

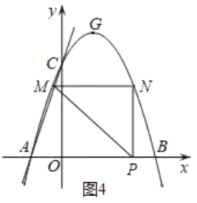
③如图4，若∠PNM＝90°，PN＝MN，
∴MN＝PN＝3e＋3，N（4e＋3，3e＋3）
解得：e＝
∴t＝AP＝OA＋OP＝1＋4e＋3＝

综上所述，存在以P，M，N为顶点的三角形为等腰直角三角形，t的值为或或．