Question

【题目】如图，已知BC⊥AC，圆心O在AC上，点M与点C分别是AC与⊙O的交点，点D是MB与⊙O的交点，点P是AD延长线与BC的交点，且ADAO＝AMAP．

（1）连接OP，证明：△ADM∽△APO；

（2）证明：PD是ΘO的切线；

（3）若AD＝24，AM＝MC，求的值．

Answer 1

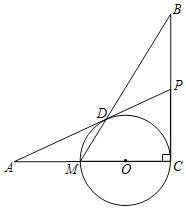
【答案】（1）见解析；（2）见解析；（3）．

【解析】

（1）根据两边成比例夹角相等两三角形相似证明即可；

（2）通过证明OD⊥PA即可；

（3）连接CD，由（1）可知：PC＝PD，由AM＝MC，推出AM＝2MO＝2R，在Rt△AOD中，OD2+AD2＝OA2，可得R2+242＝9R2，推出R＝6，推出OD＝6，MC＝12，由＝＝，可得DP＝12，再利用相似三角形的性质求出MD即可解决问题．

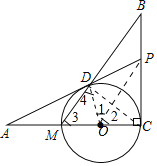
（1）证明：连接OD、OP、CD．

∵ADAO＝AMAP，

∴＝，∠A＝∠A，

∴△ADM∽△APO．

（2）∵△ADM∽△APO，

∴∠ADM＝∠APO，

∴MD∥PO，

∴∠1＝∠4，∠2＝∠3，

∵OD＝OM，

∴∠3＝∠4，

∴∠1＝∠2，

∵OP＝OP，OD＝OC，

∴△ODP≌△OCP，

∴∠ODP＝∠OCP，

∵BC⊥AC，

∴∠OCP＝90°，

∴OD⊥AP，

∴PD是⊙O的切线．

（3）连接CD．由（1）可知：PC＝PD，

∵AM＝MC，

∴AM＝2MO＝2R，

在Rt△AOD中，OD2+AD2＝OA2，

∴R2+242＝9R2，

∴R＝6，

∴OD＝6，MC＝12，

∵＝＝，

∴DP＝12，

∵O是MC的中点，

∴＝＝，

∴点P是BC的中点，

∴BP＝CP＝DP＝12，

∵MC是⊙O的直径，

∴∠BDC＝∠CDM＝90°，

在Rt△BCM中，∵BC＝2DP＝24，MC＝12，

∴BM＝12，

∵△BCM∽△CDM，

∴＝，即＝，

∴MD＝4，

∴＝＝．