题目内容
19.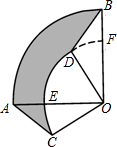 如图,把两个扇形OAB与扇形OCD的圆心重合叠放在一起,且∠AOB=∠COD,连接AC.
如图,把两个扇形OAB与扇形OCD的圆心重合叠放在一起,且∠AOB=∠COD,连接AC.(1)求证:△AOC≌△BOD;
(2)若OA=3cm,OC=2cm,弧AB的长为$\frac{3π}{2}$,弧CD的长为π,求阴影部分的面积.
分析 (1)根据90°的角可以证明,∠AOC=∠BOD,再根据同一扇形的半径相等,利用边角边定理即可证明三角形全等;
(2)根据扇形面面积公式求出阴影部分的面积.
解答 解:(1)依图有:OA=OB,OC=OD,
∵∠AOB=∠COD,
∴∠DOB=∠COA,
在△AOC与△BOD中
$\left\{\begin{array}{l}{OA=OB}\\{∠DOB=∠COA}\\{OC=OD}\end{array}\right.$,
∴△AOC≌△BOD(SAS)
(2)S阴影=S扇形OAB-S扇形OEF=S扇形OAB-S扇形OCD=$\frac{1}{2}×\frac{3π}{2}×3-\frac{1}{2}×π×2=\frac{9π}{4}-π=\frac{5π}{4}$.
点评 本题主要考查了全等三角形的判定和如何计算扇形的面积,全等三角形的证明,常用的方法有“边边边”,“边角边”,“角边角”,“角角边”,本题证明得到∠AOC=∠BOD是解题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
9.若点(-2,y1),(-1,y2),(1,y3)在反比例函数y=$\frac{4}{x}$的图象上,则下列说法正确的是( )
| A. | y1>y2>y3 | B. | y3>y2>y1 | C. | y3>y1>y2 | D. | y2>y1>y3 |
10.下列图形中,既是中心对称图形又是轴对称图形的有( )个.
①线段;②等边三角形;③矩形;④菱形;⑤平行四边形.
①线段;②等边三角形;③矩形;④菱形;⑤平行四边形.
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 2个 |