题目内容
10.已知 α、β是关于x的方程x2-2mx+m2+4m=0的两个实根(1)求m的取值范围;
(2)若α、β并且满足(α-1)(β-1)=4,求m的值.
分析 (1)根据△的意义得到△≥0,即(-2m)2-4(m2+4m)≥0,然后解不等式即可.
(2)根据根与系数的关系,得到关于m的方程,然后解方程即可.
解答 解:∵关于x的方程x2-2mx+m2+4m=0的两个实根,
∴△=(-2m)2-4(m2+4m)=-16m≥0,
解得:m≤0;
(2)∵α、β是关于x的方程x2-2mx+m2+4m=0的两个实根,
∴α+β=2m,αβ=m2+4m,
∴(α-1)(β-1)=αβ-(α+β)=m2+4m-2m=4,
解得:m=-3.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了不等式的解法和根与系数的关系.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
1.某服装店销售一款新式女式T恤,试销期间对该款不同型号女式T恤的销售量统计如下表:
该店经理如果想要了解哪种型号女式T恤销售量最大,那么他应关注的统计量是众数.
| 型号 | X | XL | XXL | XXXL |
| 销售量/件 | 1 | 8 | 5 | 1 |
18.已知a为任意整数,且(a+13)2-a2的值总可以被n(n为自然数,且n≠1)整除,则n的值为( )
| A. | 13 | B. | 26 | C. | 13或26 | D. | 13的倍数 |
5.某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送1035张照片,如果全班有x名同学,根据题意,列出方程为( )
| A. | x(x+1)=1035 | B. | $\frac{1}{2}$x(x+1)=1035 | C. | x(x-1)=1035 | D. | $\frac{1}{2}$x(x-1)=1035 |
2.绝对值是10的有理数是( )
| A. | 10 | B. | -10 | C. | ±10 | D. | 以上都对 |
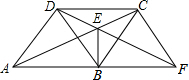 如图,四边形ABCD是菱形,点E为对角线AC上一点,连接DE并延长交AB延长线于点F.连接CF、BD、BE
如图,四边形ABCD是菱形,点E为对角线AC上一点,连接DE并延长交AB延长线于点F.连接CF、BD、BE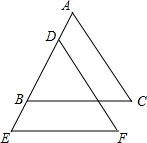 已知:如图BC∥EF,BC=EF,AB=DE;说明AC与DF相等.
已知:如图BC∥EF,BC=EF,AB=DE;说明AC与DF相等.
 矩形ABCD中,E,F,M分别为AB,BC,CD边上的点,且AB=6,BC=7,AE=3,DM=2,EF⊥FM,则BF的长为3或4.
矩形ABCD中,E,F,M分别为AB,BC,CD边上的点,且AB=6,BC=7,AE=3,DM=2,EF⊥FM,则BF的长为3或4.