题目内容
15.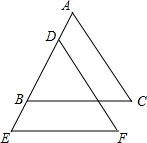 已知:如图BC∥EF,BC=EF,AB=DE;说明AC与DF相等.
已知:如图BC∥EF,BC=EF,AB=DE;说明AC与DF相等.证明:∵BC∥EF(已知)
∴∠ABC=∠DEF
在△ABC和△DEF中
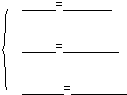
∴△ABC≌△DEF
∴AC=DF.
分析 根据两直线平行,同位角相等,可得出∠ABC=∠DEF,再利用SAS求证△ABC≌△DEF,然后利用其对边相等即可得出结论.
解答 解:∵BC∥EF(已知)
∴∠ABC=∠DEF,
在△ABC和△DEF中
$\left\{\begin{array}{l}{AB=DE}\\{∠ABC=∠DEF}\\{BC=EF}\end{array}\right.$
∴△ABC≌△DEF ( SAS)
∴AC=DF.
故答案为:DEF;AB=DE,∠ABC=∠DEF,BC=EF;△DEF;DF.
点评 此题主要考查了全等三角形的判定,理解和掌握全等三角形的判定方法是解决问题的关键.

练习册系列答案
相关题目
7.|a|=-a,则a一定是( )
| A. | 负数 | B. | 正数 | C. | 零或负数 | D. | 非负数 |
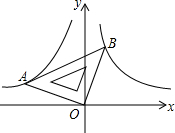 如图,一块等腰直角三角板AOB的直角顶点O与坐标原点生命,点B、A分别在第一、二象限,反比例函数y=$\frac{{k}_{1}}{x}$、y=$\frac{{k}_{2}}{x}$的图象分别经过点A、B,若点A的坐标是(-3,1),分别求出k1,k2的值.
如图,一块等腰直角三角板AOB的直角顶点O与坐标原点生命,点B、A分别在第一、二象限,反比例函数y=$\frac{{k}_{1}}{x}$、y=$\frac{{k}_{2}}{x}$的图象分别经过点A、B,若点A的坐标是(-3,1),分别求出k1,k2的值.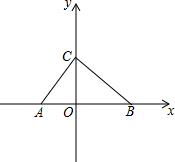 如图所示,点A、B、C的坐标分别为(-$\sqrt{2}$,0),(2$\sqrt{2}$,0),(0,2).
如图所示,点A、B、C的坐标分别为(-$\sqrt{2}$,0),(2$\sqrt{2}$,0),(0,2).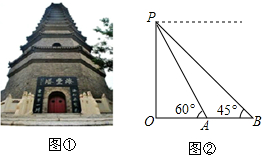 海丰塔是无棣灿烂文化的象征(如图①),喜爱数学实践活动的小伟查资料得知:海丰塔,史称唐塔,原名大觉寺塔,始建于唐贞观十三年(公元639年),碑记为“尉迟敬德监建”,距今已1300多年,被誉为冀鲁三胜之一.小伟决定用自己所学习的知识测量海丰塔的高度.如图②,他利用测角仪站在B处测得海丰塔最高点P的仰角为45°,又前进了18米到达A处,在A处测得P的仰角为60°.请你帮助小伟算算海丰塔的高度.(测角仪高度忽略不计,$\sqrt{3}$≈1.7,结果保留整数).
海丰塔是无棣灿烂文化的象征(如图①),喜爱数学实践活动的小伟查资料得知:海丰塔,史称唐塔,原名大觉寺塔,始建于唐贞观十三年(公元639年),碑记为“尉迟敬德监建”,距今已1300多年,被誉为冀鲁三胜之一.小伟决定用自己所学习的知识测量海丰塔的高度.如图②,他利用测角仪站在B处测得海丰塔最高点P的仰角为45°,又前进了18米到达A处,在A处测得P的仰角为60°.请你帮助小伟算算海丰塔的高度.(测角仪高度忽略不计,$\sqrt{3}$≈1.7,结果保留整数).