题目内容
13. 如图,将矩形ABCD沿EF折叠,使点B,D重合,已知AB=3,AD=4,则
如图,将矩形ABCD沿EF折叠,使点B,D重合,已知AB=3,AD=4,则①DE=DF;②DF=EF;③△DCF≌△DGE;④EF=$\frac{15}{4}$.
上面结论正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 如图作EM⊥BC于M,首先证明△DEG≌△DFC,由此可以判断①③正确.设DF=FB=x,则CF=4-x,在RT△DCF中,根据DF2=CD2+CF2,列出方程求出x,在RT△EMF中求出EM,MF利用勾股定理即可求出EF,即可判断④正确.②错误,可以用反证法证明.
解答 解;如图作EM⊥BC于M.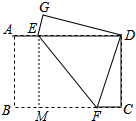
∵四边形ABCD是矩形,四边形EFDG是由四边形ABEF翻折,
∴∠ADC=∠GDF=∠C=∠G=90°,DC=DG=AB=3,AD=BC=4
∴∠EDG=∠CDF,
在△DEG和△DFC中,
$\left\{\begin{array}{l}{∠G=∠C}\\{DG=DC}\\{∠EDG=∠CDF}\end{array}\right.$,
∴△DEG≌△DFC.故③正确,
∴DE=DF,故①正确,
设DF=FB=x,则CF=4-x,
在RT△DCF中,∵DF2=CD2+CF2,
∴x2=(4-x)2+32,
∴x=$\frac{25}{8}$,
∴DE=DF=$\frac{25}{8}$,
∵四边形AEMB是矩形,
∴AE=BM=$\frac{7}{8}$,ME=AB=3,
∴MF=BC-BM-CF=4-$\frac{7}{8}$-(4-$\frac{25}{8}$)=$\frac{9}{4}$,
在RT△EFM中,EF=$\sqrt{E{M}^{2}+M{F}^{2}}$=$\frac{15}{4}$.故④正确,
②错误.假设DF=EF,∵DE=DF,
∴EF=DE=DF,
∴△DEF是等边三角形,
∴∠DFE=60°,
∴∠BFE=∠DFE=∠DFC=60°,
这显然不可能,假设不成立,故②错误.
故正确的有3个,选C
点评 本题考查翻折变换、全等三角形的判定和性质、勾股定理等知识,解题的关键是正确寻找全等三角形,学会添加常用辅助线,属于中考常考题型.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 所示的不完整统计表和扇形统计图:
所示的不完整统计表和扇形统计图:| 八年级2班参加球类活动人数统计表 | |||||
| 项目 | 篮球 | 足球 | 乒乓球 | 排球 | 羽毛球 |
| 人数 | a | 6 | 5 | 7 | 6 |
(1)a=16,b=17.5;
(2)该校八年级学生共有600人,则该年级参加足球活动的人数约90人;
(3)该班参加乒乓球活动的5位同学中,有3位男同学(A,B,C)和2位女同学(D,E),现准备从中选取两名同学组成双打组合,用树状图或列表法求恰好选出一男一女组成混合双打组合的概率.
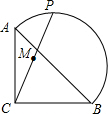 如图,在等腰Rt△ABC中,AC=BC=2$\sqrt{2}$,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是( )
如图,在等腰Rt△ABC中,AC=BC=2$\sqrt{2}$,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是( )| A. | $\sqrt{2}$π | B. | π | C. | 2$\sqrt{2}$ | D. | 2 |
| A. | $\sqrt{9}$ | B. | $\sqrt{24}$ | C. | $\sqrt{30}$ | D. | $\sqrt{\frac{2}{3}}$ |
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )| A. | a>0 | B. | c<0 | ||
| C. | 3是方程ax2+bx+c=0的一个根 | D. | 当x<1时,y随x的增大而减小 |
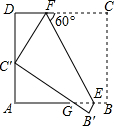 如图,正方形ABCD的边长为3,E、F分别是AB、CD上的点,且∠CFE=60°,将四边形BCFE沿EF翻折,得到B′C′FE,C′恰好落在AD边上,B′C′交AB于点G,则GE的长是( )
如图,正方形ABCD的边长为3,E、F分别是AB、CD上的点,且∠CFE=60°,将四边形BCFE沿EF翻折,得到B′C′FE,C′恰好落在AD边上,B′C′交AB于点G,则GE的长是( )| A. | 3$\sqrt{3}$-4 | B. | 4$\sqrt{2}$-5 | C. | 4-2$\sqrt{3}$ | D. | 5-2$\sqrt{3}$ |
