题目内容
7.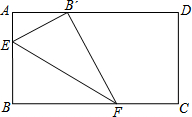 如图,在矩形ABCD中,AB=8.将矩形的一角折叠,使点B落在边AD上的B′点处,若AB′=4,则折痕EF的长度为5$\sqrt{5}$.
如图,在矩形ABCD中,AB=8.将矩形的一角折叠,使点B落在边AD上的B′点处,若AB′=4,则折痕EF的长度为5$\sqrt{5}$.
分析 作B′M⊥BC,首先在△AEB′中,设BE=x,运用勾股定理解方程求出BE,然后在△B′MF中,运用勾股定理求出B′F,再在△BEF中运用勾股定理求出EF.
解答 解:如图,作B′M⊥BC,
根据折叠的性质,BE=B′E,BF=B′F,
在Rt△AEB′中,设BE=x,则x2=(8-x)2+42
解得:x=5,
∵四边形ABMB′是矩形,
∴BM=AB′=4,B′M=AB=8,
设BF=y,则82+(y-4)2=y2,
解得:y=10,
∵BE=5,BF=10,
∴EF=5$\sqrt{5}$.
点评 本题主要考查了折叠的性质和勾股定理的综合运用,作B′M⊥BC,构造直角三角形求出BF是解决问题的关键.

练习册系列答案
相关题目
17.在今年的中招体育考试中,我校甲、乙、丙、丁四个班级的平均分完全一样,方差分别为:S甲2=8.5,S乙2=21.7,S丙2=15,S丁2=17.2,则四个班体考成绩最稳定的是( )
| A. | 甲班 | B. | 乙班 | C. | 丙班 | D. | 丁班 |
18. 如图,以G(0,1)为圆心,2为半径的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为圆G上一动点,CF⊥AE于F,当点E从点B出发顺时针运动到点D时,点F经过的路径长为( )
如图,以G(0,1)为圆心,2为半径的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为圆G上一动点,CF⊥AE于F,当点E从点B出发顺时针运动到点D时,点F经过的路径长为( )
 如图,以G(0,1)为圆心,2为半径的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为圆G上一动点,CF⊥AE于F,当点E从点B出发顺时针运动到点D时,点F经过的路径长为( )
如图,以G(0,1)为圆心,2为半径的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为圆G上一动点,CF⊥AE于F,当点E从点B出发顺时针运动到点D时,点F经过的路径长为( )| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{3}}}{4}$ | D. | $\frac{{\sqrt{3}}}{6}$ |
15.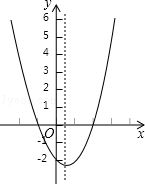 二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
 二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )| A. | 函数有最小值 | B. | 对称轴是直线x=$\frac{1}{2}$ | ||
| C. | 当-1<x<2时,y>0 | D. | 当x<$\frac{1}{2}$,y随x的增大而减小 |
17.-3的倒数是( )
| A. | 3 | B. | ±3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
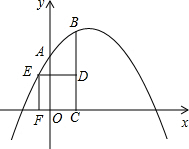 如图,抛物线y=-$\frac{1}{2}$x2+bx+c过A(0,2),B(1,3),CB⊥x轴于点C,四边形CDEF为正方形,点D在线段BC上,点E在此抛物线上,且在直线BC的左侧,则正方形CDEF的边长为$\frac{-3+\sqrt{33}}{2}$.
如图,抛物线y=-$\frac{1}{2}$x2+bx+c过A(0,2),B(1,3),CB⊥x轴于点C,四边形CDEF为正方形,点D在线段BC上,点E在此抛物线上,且在直线BC的左侧,则正方形CDEF的边长为$\frac{-3+\sqrt{33}}{2}$.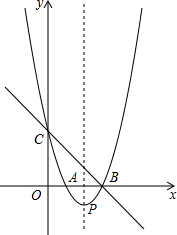 如图(1),直线y=-x+3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.
如图(1),直线y=-x+3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.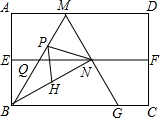 如图,四边形ABCD是矩形纸片,AB=2.对折矩形纸片ABCD,使AD与BC重合,折痕为EF;展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕BM与EF相交于点Q;再次展平,连接BN,MN,延长MN交BC于点G.有如下结论:
如图,四边形ABCD是矩形纸片,AB=2.对折矩形纸片ABCD,使AD与BC重合,折痕为EF;展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕BM与EF相交于点Q;再次展平,连接BN,MN,延长MN交BC于点G.有如下结论: