题目内容
12. 已知线段AB=12cm,C为线段AB上任一点,E是AC的中点,F为BC的中点,求线段EF的长度.
已知线段AB=12cm,C为线段AB上任一点,E是AC的中点,F为BC的中点,求线段EF的长度.
分析 根据线段中点的定义由E是AC的中点,N是BC的中点得到EC=$\frac{1}{2}$AC,FC=$\frac{1}{2}$BC,则EC+FC=$\frac{1}{2}$(AC+BC)=$\frac{1}{2}$AB,即EF=$\frac{1}{2}$AB,然后把AB的长代入计算即可.
解答 ∵点C是线段AB上一点,E是AC的中点,N是BC的中点,
∴EC=$\frac{1}{2}$AC,FC=$\frac{1}{2}$BC,
∴EC+FC=$\frac{1}{2}$(AC+BC)=$\frac{1}{2}$AB,即EF=$\frac{1}{2}$AB,
∵AB=12cm,
∴EF=$\frac{1}{2}$×12cm=6cm.
点评 本题考查了两点间的距离:两点间的线段的长度叫这两点间的距离.也考查了线段中点的定义,找出线段间的数量关系是解决此类问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.下列事件属于不可能事件的是( )
| A. | 抛一次骰子,向上的一面是6点 | B. | 打开电视机,正在转播足球比赛 | ||
| C. | 地球上,向上抛的篮球会下落 | D. | 从只有红球的袋子中,摸出1个白球 |
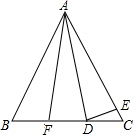 如图,△ABC中,∠B=∠C,AB=AC,D、F在BC边上,BF=CD,E在AC边上,∠ADE=∠AED,∠EDC=23°,则∠FAC=46°.
如图,△ABC中,∠B=∠C,AB=AC,D、F在BC边上,BF=CD,E在AC边上,∠ADE=∠AED,∠EDC=23°,则∠FAC=46°.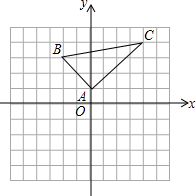 如图,在平面直角坐标系中,A(0,1),B(-2,3),C(4,4).
如图,在平面直角坐标系中,A(0,1),B(-2,3),C(4,4).