题目内容
20.用代入法解三元一次方程组$\left\{\begin{array}{l}{2x+y+3z=13}\\{3x+2y-z=16}\\{x+3y-5z=10}\end{array}\right.$.分析 方程组利用代入消元法求出解即可.
解答 解:$\left\{\begin{array}{l}{2x+y+3z=13①}\\{3x+2y-z=16②}\\{x+3y-5z=10③}\end{array}\right.$,
由②得:z=3x+2y-16④,
把④代入①得:2x+y+9x+6y-48=13,即11x+7y=61⑤;
把④代入③得:x+3y-15x-10y+80=10,即2x+y=10⑥,
⑥×7-⑤得:3x=9,即x=3,
把x=3代入⑥得:y=4,
把x=3,y=4代入④得:z=1,
则方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=4}\\{z=1}\end{array}\right.$.
点评 此题考查了解三元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
9.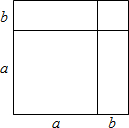 如图,大正方形的边长为a+b,用两种不同的方法计算这个大正方形的面积,可以推导出的公式是( )
如图,大正方形的边长为a+b,用两种不同的方法计算这个大正方形的面积,可以推导出的公式是( )
 如图,大正方形的边长为a+b,用两种不同的方法计算这个大正方形的面积,可以推导出的公式是( )
如图,大正方形的边长为a+b,用两种不同的方法计算这个大正方形的面积,可以推导出的公式是( )| A. | (a+b)(a-b)=a2-b2 | B. | (a+b)2=a2+2ab+b2 | C. | (a-b)2=a2-2ab+b2 | D. | (a+b)2-(a-b)2=4ab |
 已知线段AB=12cm,C为线段AB上任一点,E是AC的中点,F为BC的中点,求线段EF的长度.
已知线段AB=12cm,C为线段AB上任一点,E是AC的中点,F为BC的中点,求线段EF的长度.