题目内容
17.若等腰三角形的两边的长分别是5cm、7cm,则它的周长为17或19cm.分析 根据等腰三角形的性质,分两种情况:①当腰长为5cm时,②当腰长为7cm时,分别进行求解即可.
解答 解:①当腰长为5cm时,三角形的三边分别为5cm,5cm,7cm,符合三角形的三关系,则三角形的周长=5+5+7=17(cm);
②当腰长为7cm时,三角形的三边分别为5cm,7cm,7cm,符合三角形的三关系,则三角形的周长=5+7+7=19(cm);
故答案为:17或19.
点评 此题主要考查学生对等腰三角形的性质及三角形的三边关系的掌握情况.已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形.

练习册系列答案
相关题目
9.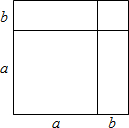 如图,大正方形的边长为a+b,用两种不同的方法计算这个大正方形的面积,可以推导出的公式是( )
如图,大正方形的边长为a+b,用两种不同的方法计算这个大正方形的面积,可以推导出的公式是( )
 如图,大正方形的边长为a+b,用两种不同的方法计算这个大正方形的面积,可以推导出的公式是( )
如图,大正方形的边长为a+b,用两种不同的方法计算这个大正方形的面积,可以推导出的公式是( )| A. | (a+b)(a-b)=a2-b2 | B. | (a+b)2=a2+2ab+b2 | C. | (a-b)2=a2-2ab+b2 | D. | (a+b)2-(a-b)2=4ab |
7.将抛物线y=2(x-7)2+3平移,使平移后的函数图象顶点落在y轴上,则下列平移正确的是( )
| A. | 向上平移3个单位 | B. | 向下平移3个单位 | C. | 向左平移7个单位 | D. | 向右平移7个单位 |
 已知线段AB=12cm,C为线段AB上任一点,E是AC的中点,F为BC的中点,求线段EF的长度.
已知线段AB=12cm,C为线段AB上任一点,E是AC的中点,F为BC的中点,求线段EF的长度.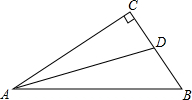 如图,在△ABC中,∠C是直角,AD平分∠BAC,交BC于点D;如果AB=8,CD=2,那么△ABD的面积等于( )
如图,在△ABC中,∠C是直角,AD平分∠BAC,交BC于点D;如果AB=8,CD=2,那么△ABD的面积等于( )