题目内容
4.小明从家里骑自行车到学校,每小时骑15km,可早到10分钟,每小时骑12km就会迟到5分钟.问他家到学校的路程是多少km?设他家到学校的路程是xkm,则据题意列出的方程是AA:$\frac{x}{15}+\frac{10}{60}=\frac{x}{12}-\frac{5}{60}$ B:$\frac{x}{15}-\frac{10}{60}=\frac{x}{12}+\frac{5}{60}$ C:$\frac{x}{15}-\frac{10}{60}=\frac{x}{12}-\frac{5}{60}$ D$\frac{x}{15}+10=\frac{x}{12}-5$
导学探究
(1)路程,速度,时间的关系是路程=速度×时间
(2)规定的到校时间是$\frac{x}{15}$+$\frac{10}{60}$或$\frac{x}{12}$-$\frac{5}{60}$.
分析 设他家到学校的路程是xkm,根据每小时骑15km,可早到10分钟,每小时骑12km就会迟到5分钟,列方程即可.
(1)路程,速度,时间的关系是路程=速度×时间;
(2)规定的到校时间是$\frac{x}{15}$+$\frac{10}{60}$或$\frac{x}{12}$-$\frac{5}{60}$.
解答 解:设他家到学校的路程是x km,
由题意得,$\frac{x}{15}$+$\frac{10}{60}$=$\frac{x}{12}$-$\frac{5}{60}$.
故选A.
(1)路程,速度,时间的关系是路程=速度×时间;
(2)规定的到校时间是$\frac{x}{15}$+$\frac{10}{60}$或$\frac{x}{12}$-$\frac{5}{60}$.
故答案为A;路程=速度×时间;$\frac{x}{15}$+$\frac{10}{60}$,$\frac{x}{12}$-$\frac{5}{60}$.
点评 本题考查了一元一次方程的应用,解答本题的关键是读懂题意,找出合适的等量关系,列方程.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.以下列长度的三条线段为边,不能组成直角三角形的是( )
| A. | 3,4,5 | B. | 6,8,10 | C. | 5,12,13 | D. | 1,1,2 |
9.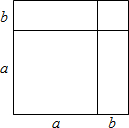 如图,大正方形的边长为a+b,用两种不同的方法计算这个大正方形的面积,可以推导出的公式是( )
如图,大正方形的边长为a+b,用两种不同的方法计算这个大正方形的面积,可以推导出的公式是( )
 如图,大正方形的边长为a+b,用两种不同的方法计算这个大正方形的面积,可以推导出的公式是( )
如图,大正方形的边长为a+b,用两种不同的方法计算这个大正方形的面积,可以推导出的公式是( )| A. | (a+b)(a-b)=a2-b2 | B. | (a+b)2=a2+2ab+b2 | C. | (a-b)2=a2-2ab+b2 | D. | (a+b)2-(a-b)2=4ab |
13.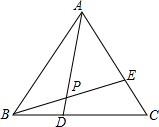 如图,△ABC是等边三角形,D,E分别在BC和AC上,BD=CE,连接BE交AD于P点,则∠APB的度数是( )
如图,△ABC是等边三角形,D,E分别在BC和AC上,BD=CE,连接BE交AD于P点,则∠APB的度数是( )
 如图,△ABC是等边三角形,D,E分别在BC和AC上,BD=CE,连接BE交AD于P点,则∠APB的度数是( )
如图,△ABC是等边三角形,D,E分别在BC和AC上,BD=CE,连接BE交AD于P点,则∠APB的度数是( )| A. | 60° | B. | 90° | C. | 120° | D. | 150° |
14. 如图,把一根直尺与一块三角板叠放在一起,若∠1=65°,则∠2的度数是( )
如图,把一根直尺与一块三角板叠放在一起,若∠1=65°,则∠2的度数是( )
 如图,把一根直尺与一块三角板叠放在一起,若∠1=65°,则∠2的度数是( )
如图,把一根直尺与一块三角板叠放在一起,若∠1=65°,则∠2的度数是( )| A. | 25° | B. | 35° | C. | 45° | D. | 65° |
 如图C,D是线段AB上的两点,M,N分别是AC,BD的中点,若CD=6cm,MN=9cm,求线段AB的长.
如图C,D是线段AB上的两点,M,N分别是AC,BD的中点,若CD=6cm,MN=9cm,求线段AB的长. 已知线段AB=12cm,C为线段AB上任一点,E是AC的中点,F为BC的中点,求线段EF的长度.
已知线段AB=12cm,C为线段AB上任一点,E是AC的中点,F为BC的中点,求线段EF的长度.