题目内容
2.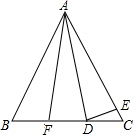 如图,△ABC中,∠B=∠C,AB=AC,D、F在BC边上,BF=CD,E在AC边上,∠ADE=∠AED,∠EDC=23°,则∠FAC=46°.
如图,△ABC中,∠B=∠C,AB=AC,D、F在BC边上,BF=CD,E在AC边上,∠ADE=∠AED,∠EDC=23°,则∠FAC=46°.
分析 首先利用SAS证得△ABF≌△ACD,得到∠BAF=∠CAD,然后设∠B=∠C=x,利用三角形内角和定理可知∠BAC=180°-x,利用三角形的外角性质可知∠ADE=∠AED=x+23°,并表示出∠CAD与∠BAF,再利用∠FAC=∠BAC-∠BAF进行计算即可.
解答 解:在△ABF与△ACD中,
$\left\{\begin{array}{l}{AB=AC}\\{∠B=∠C}\\{BF=CD}\end{array}\right.$,
∴△ABF≌△ACD(SAS),
∴∠BAF=∠CAD,
设∠B=∠C=x,
∴∠BAC=180°-2x,
∵∠EDC=23°,
∴∠ADE=∠AED=∠EDC+∠C=x+23°,
∴∠CAD=180°-∠ADE-∠AED=180°-(x+23°)-(x+23°)=134°-2x,
∴∠BAF=∠CAD=134°-2x,
∴∠FAC=∠BAC-∠BAF=(180°-2x)-(134°-2x)=46°,
故答案为:46.
点评 本题考查了等腰三角形的性质,全等三角形的判定与性质,三角形内角和定理,三角形的外角性质等知识,正确识图,理清图形中各角之间的关系是解题的关键.

练习册系列答案
相关题目
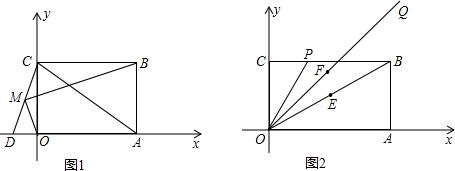
 如图,由两个等宽的矩形叠合而得到的四边形ABCD是菱形吗?证明你的结论.
如图,由两个等宽的矩形叠合而得到的四边形ABCD是菱形吗?证明你的结论. 如图C,D是线段AB上的两点,M,N分别是AC,BD的中点,若CD=6cm,MN=9cm,求线段AB的长.
如图C,D是线段AB上的两点,M,N分别是AC,BD的中点,若CD=6cm,MN=9cm,求线段AB的长. 已知线段AB=12cm,C为线段AB上任一点,E是AC的中点,F为BC的中点,求线段EF的长度.
已知线段AB=12cm,C为线段AB上任一点,E是AC的中点,F为BC的中点,求线段EF的长度.