题目内容
1.一列火车往返于芜湖、杭州两个城市,中途经过宣城、广德、长兴南和德清西4个站点(共6个站点),不同的车站往返需要不同的车票.(1)共有多少种不同的车票?
(2)一列火车往返A、B两个城市,如果共有n(n≥3)个站点,则需要多少种不同的车票?
分析 两站之间的往返车票各一种,即两种,n个车站每两站之间有两种,则n个车站的票的种类数=n(n-1)种,n=6时,即6个车站,代入上式即可求得票的种数.
解答 解:(1)两站之间的往返车票各一种,即两种,则6个车站的票的种类数=6×5=30(种);
(2)n个车站的票的种类数=n(n-1)种.
点评 本题考查了直线、射线、线段,解决本题的关键是在线段的计数时,应注重分类讨论的方法计数,做到不遗漏,不重复.

练习册系列答案
相关题目
9.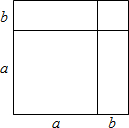 如图,大正方形的边长为a+b,用两种不同的方法计算这个大正方形的面积,可以推导出的公式是( )
如图,大正方形的边长为a+b,用两种不同的方法计算这个大正方形的面积,可以推导出的公式是( )
 如图,大正方形的边长为a+b,用两种不同的方法计算这个大正方形的面积,可以推导出的公式是( )
如图,大正方形的边长为a+b,用两种不同的方法计算这个大正方形的面积,可以推导出的公式是( )| A. | (a+b)(a-b)=a2-b2 | B. | (a+b)2=a2+2ab+b2 | C. | (a-b)2=a2-2ab+b2 | D. | (a+b)2-(a-b)2=4ab |
13.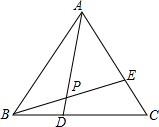 如图,△ABC是等边三角形,D,E分别在BC和AC上,BD=CE,连接BE交AD于P点,则∠APB的度数是( )
如图,△ABC是等边三角形,D,E分别在BC和AC上,BD=CE,连接BE交AD于P点,则∠APB的度数是( )
 如图,△ABC是等边三角形,D,E分别在BC和AC上,BD=CE,连接BE交AD于P点,则∠APB的度数是( )
如图,△ABC是等边三角形,D,E分别在BC和AC上,BD=CE,连接BE交AD于P点,则∠APB的度数是( )| A. | 60° | B. | 90° | C. | 120° | D. | 150° |
11. 如图,已知BC=EC,∠BCE=∠ACD,如果只添加一个条件使△ABC≌△DEC,则添加的条件不能为( )
如图,已知BC=EC,∠BCE=∠ACD,如果只添加一个条件使△ABC≌△DEC,则添加的条件不能为( )
 如图,已知BC=EC,∠BCE=∠ACD,如果只添加一个条件使△ABC≌△DEC,则添加的条件不能为( )
如图,已知BC=EC,∠BCE=∠ACD,如果只添加一个条件使△ABC≌△DEC,则添加的条件不能为( )| A. | AB=DE | B. | ∠B=∠E | C. | AC=DC | D. | ∠A=∠D |
 已知线段AB=12cm,C为线段AB上任一点,E是AC的中点,F为BC的中点,求线段EF的长度.
已知线段AB=12cm,C为线段AB上任一点,E是AC的中点,F为BC的中点,求线段EF的长度.