题目内容
11.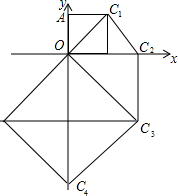 如图,点A是y轴上的一点,以线段OA为边作第1个正方形,得到对角线OC1,再以OC1为边作第2个正方形,得到对角线OC2,再以OC2为边作第3个正方形,得到对角线OC3,再以OC3为边作第4个正方形,得到对角线OC4,…,以此类推,得到正方形对角线OC2017,若OA的长度为1,则点C2017的坐标是(21008,21008).
如图,点A是y轴上的一点,以线段OA为边作第1个正方形,得到对角线OC1,再以OC1为边作第2个正方形,得到对角线OC2,再以OC2为边作第3个正方形,得到对角线OC3,再以OC3为边作第4个正方形,得到对角线OC4,…,以此类推,得到正方形对角线OC2017,若OA的长度为1,则点C2017的坐标是(21008,21008).
分析 根据Cn点的排布规律,写出部分Cn点的坐标,根据点的坐标的变化找出变化规律“C8n+1(24n,24n),C8n+2(24n+1,0),C8n+3(24n+1,-24n+1),C8n+4(0,-24n+2),C8n+5(-24n+2,-24n+2),C4n+6(-24n+3,0),C4n+7(-24n+3,24n+3),C8n+8(0,24(n+1))”,依次变化规律即可得出结论.
解答 解:观察,发现规律:C1(1,1),C2(2,0),C3(2,-2),C4(0,-4),C5(-4,-4),C6(-8,0),C7(-8,8),C8(0,16),C9(16,16),…,
∴C8n+1(24n,24n),C8n+2(24n+1,0),C8n+3(24n+1,-24n+1),C8n+4(0,-24n+2),C8n+5(-24n+2,-24n+2),C4n+6(-24n+3,0),C4n+7(-24n+3,24n+3),C8n+8(0,24(n+1))(n为自然数).
∵2017=252×8+1,
∴点C2017的坐标是(24×252,24×252)=(21008,21008).
故答案为:(21008,21008).
点评 本题考查了规律型中的点的坐标变化,解题的关键是找出规律“C8n+1(24n,24n),C8n+2(24n+1,0),C8n+3(24n+1,-24n+1),C8n+4(0,-24n+2),C8n+5(-24n+2,-24n+2),C4n+6(-24n+3,0),C4n+7(-24n+3,24n+3),C8n+8(0,24(n+1))”.本题属于中档题,难度不大,解决该题型题目时,列出部分点Cn的坐标,根据坐标的变化找出变化规律是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.方程组$\left\{\begin{array}{l}{x-y=1}\\{x+y=3}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ |
6.如果a<b<0,那么不等式ax<b的解集是( )
| A. | x<$\frac{b}{a}$ | B. | x>$\frac{b}{a}$ | C. | x<-$\frac{b}{a}$ | D. | x>-$\frac{b}{a}$ |

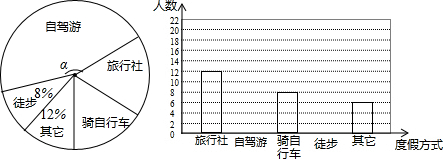
 如图,AB为⊙O的直径,点C是$\widehat{AB}$上一点,点D为$\widehat{AC}$的中点,弦AC、BD交于点E,F为BD延长线上一点,且FA是⊙O的切线,
如图,AB为⊙O的直径,点C是$\widehat{AB}$上一点,点D为$\widehat{AC}$的中点,弦AC、BD交于点E,F为BD延长线上一点,且FA是⊙O的切线,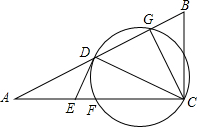 如图所示,在△ABC中,∠ACB=90°,D,F分别为AB,AC的中点,过D,F,C三点的⊙O交AB于点G,连接CG,CD,作DE⊥CD,交AC于点E.
如图所示,在△ABC中,∠ACB=90°,D,F分别为AB,AC的中点,过D,F,C三点的⊙O交AB于点G,连接CG,CD,作DE⊥CD,交AC于点E.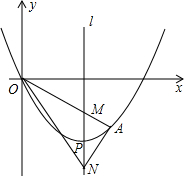 如图,抛物线y=$\frac{1}{4}$(x-4)2-4的顶点为P,M,N均在对称轴上,且PM=PN,延长OM交抛物线于点A,求证:∠ANM=∠ONM.
如图,抛物线y=$\frac{1}{4}$(x-4)2-4的顶点为P,M,N均在对称轴上,且PM=PN,延长OM交抛物线于点A,求证:∠ANM=∠ONM.