题目内容
3.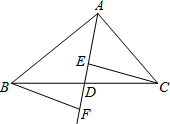 已知命题:如图,在△ABC中,点D是BC的点,作射线AD,在线段AD及其延长线上分别取点E、F,连结CE、BF,则△BDF≌△CDF,判断这个命题是真命题还是假命题?如果是真命题,请给出证明;如果是假命题,请添加一个适当的条件(不添加任何辅助线)使它成为真命题.你所添加的条件是:CE∥BF,并加以证明.
已知命题:如图,在△ABC中,点D是BC的点,作射线AD,在线段AD及其延长线上分别取点E、F,连结CE、BF,则△BDF≌△CDF,判断这个命题是真命题还是假命题?如果是真命题,请给出证明;如果是假命题,请添加一个适当的条件(不添加任何辅助线)使它成为真命题.你所添加的条件是:CE∥BF,并加以证明.
分析 首先容易判断该命题是假命题;经分析探究增加的一个条件可以是CE∥BF,也可以是DE=DF,选择其中任意一个即可解决问题.
解答  解:如图,该命题是假命题;添加条件:CE∥BF;证明如下:
解:如图,该命题是假命题;添加条件:CE∥BF;证明如下:
∵CE∥BF,
∴∠DBF=∠DCE;
在△BDF与△CDE中,
$\left\{\begin{array}{l}{∠DBF=∠DCE}\\{BD=CD}\\{∠DBF=∠DCE}\end{array}\right.$,
∴△BDF≌△CDE(ASA).
点评 该题是一道条件探究型几何题;主要考查了全等三角形的判定方法及其应用问题;对探究、发现能力也提出了一定的要求.

练习册系列答案
相关题目
15. 如图,在?ABCD中,点E、F分别在AB、CD上,且AE=CF,则四边形BFDE不可能是( )
如图,在?ABCD中,点E、F分别在AB、CD上,且AE=CF,则四边形BFDE不可能是( )
 如图,在?ABCD中,点E、F分别在AB、CD上,且AE=CF,则四边形BFDE不可能是( )
如图,在?ABCD中,点E、F分别在AB、CD上,且AE=CF,则四边形BFDE不可能是( )| A. | 矩形 | B. | 菱形 | C. | 梯形 | D. | 平行四边形 |
13.下列计算正确的是( )
| A. | a3•a2=a6 | B. | (-3pq)2=-6p2q2 | C. | (-bc)4÷(-bc)2=b2c2 | D. | a+a=a2 |
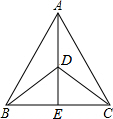 如图,在△ABC中,AB=AC,DB=DC,AD的延长线交BC于点E,求证:∠BAE=∠CAE.
如图,在△ABC中,AB=AC,DB=DC,AD的延长线交BC于点E,求证:∠BAE=∠CAE.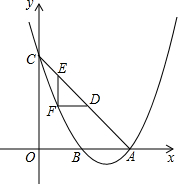 如图,当x=2时,抛物线y=ax2+bx+c取得最小值-1,并且抛物线与y轴交于点C(0,3),与x轴交于点A、B.
如图,当x=2时,抛物线y=ax2+bx+c取得最小值-1,并且抛物线与y轴交于点C(0,3),与x轴交于点A、B.