题目内容
6.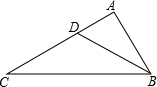 如图,点D是△ABC的边AC的上一点,且∠ABD=∠C;如果$\frac{AD}{CD}$=$\frac{1}{2}$,那么$\frac{BD}{BC}$=$\frac{\sqrt{3}}{3}$.
如图,点D是△ABC的边AC的上一点,且∠ABD=∠C;如果$\frac{AD}{CD}$=$\frac{1}{2}$,那么$\frac{BD}{BC}$=$\frac{\sqrt{3}}{3}$.
分析 先证明△ADB∽△ABC,则利用相似比得到$\frac{BD}{BC}$=$\frac{AD}{AB}$=$\frac{AB}{AC}$,再设AD=x,CD=2x,则AC=3x,则利用相似比可表示出AB=$\sqrt{3}$x,然后计算$\frac{BD}{BC}$的值.
解答 解:∵∠ABD=∠C,
而∠DAB=∠BAC,
∴△ADB∽△ABC,
∴$\frac{BD}{BC}$=$\frac{AD}{AB}$=$\frac{AB}{AC}$,
由$\frac{AD}{CD}$=$\frac{1}{2}$,设AD=x,CD=2x,则AC=3x,
∴$\frac{x}{AB}$=$\frac{AB}{3x}$,
∴AB=$\sqrt{3}$x,
∴$\frac{BD}{BC}$=$\frac{x}{\sqrt{3}x}$=$\frac{\sqrt{3}}{3}$.
故答案为$\frac{\sqrt{3}}{3}$.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;运用相似三角形的性质时只要利用相似比计算相应线段的长.解决本题的关键是设AD=x,CD=2x,然后用x表示出AB的长.

练习册系列答案
相关题目
1. 如图,下列语句正确的是( )
如图,下列语句正确的是( )
 如图,下列语句正确的是( )
如图,下列语句正确的是( )| A. | 线段AB与线段BC是同一条线段 | B. | 直线AB与直线是BC同一条直线 | ||
| C. | 点A在线段BC上 | D. | 点C在射线BA上 |
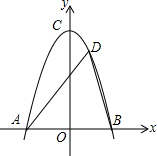 如图,某公路隧道横截面为抛物线,其最大高度为8米,以隧道底部宽AB所在直线为x轴,以AB垂直平分线为y轴建立如图所示的平面直角坐标系,抛物线解析式为y=-$\frac{1}{2}{x}^{2}+b$,则隧道底部宽AB8米.
如图,某公路隧道横截面为抛物线,其最大高度为8米,以隧道底部宽AB所在直线为x轴,以AB垂直平分线为y轴建立如图所示的平面直角坐标系,抛物线解析式为y=-$\frac{1}{2}{x}^{2}+b$,则隧道底部宽AB8米.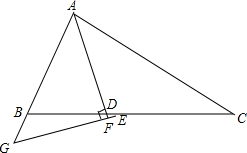 已知:△ABC中,∠ABC=2∠ACB,AD是∠BAC的角平分线,E是BC的中点,过E作EF⊥AD交AD的延长线于F,交AB的延长线于G,求证:BD=2BG.
已知:△ABC中,∠ABC=2∠ACB,AD是∠BAC的角平分线,E是BC的中点,过E作EF⊥AD交AD的延长线于F,交AB的延长线于G,求证:BD=2BG.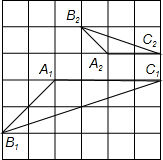 学习相似三角形和解直角三角形的相关内容后,张老师请同学们交流这样的一个问题:“如图,在正方形网格上有△A1B1C1和△A2B2C2,这两个三角形是否相似?”.那么你认为△A1B1C1和△A2B2C2相似.(填相似或不相似);理由是$\frac{{A}_{1}{B}_{1}}{{A}_{2}{B}_{2}}$=$\frac{{B}_{1}{C}_{1}}{{B}_{2}{C}_{2}}$=$\frac{{A}_{1}{C}_{1}}{{A}_{2}{C}_{2}}$.
学习相似三角形和解直角三角形的相关内容后,张老师请同学们交流这样的一个问题:“如图,在正方形网格上有△A1B1C1和△A2B2C2,这两个三角形是否相似?”.那么你认为△A1B1C1和△A2B2C2相似.(填相似或不相似);理由是$\frac{{A}_{1}{B}_{1}}{{A}_{2}{B}_{2}}$=$\frac{{B}_{1}{C}_{1}}{{B}_{2}{C}_{2}}$=$\frac{{A}_{1}{C}_{1}}{{A}_{2}{C}_{2}}$.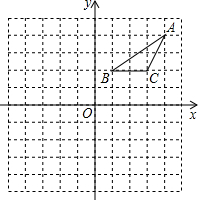 在正方形网格中,建立如图所示的平面直角坐标系xOy,△ABC的三个顶点都在格点上,点A的坐标(4,4),请解答下列问题:
在正方形网格中,建立如图所示的平面直角坐标系xOy,△ABC的三个顶点都在格点上,点A的坐标(4,4),请解答下列问题: