题目内容
1.将y=x2-2x-3沿y轴翻折得抛物线C1,求C1的解析式.分析 关于y轴对称的两点纵坐标相同,横坐标互为相反数.
解答 解:根据题意,得
抛物线C1的解析式为:y=(-x)2-2(-x)-3=x2+2x-3.即y=x2+2x-3.
点评 本题考查了二次函数图象与几何变换.
总结:关于x轴对称的两点横坐标相同,纵坐标坐标互为相反数.
关于y轴对称的两点纵坐标相同,横坐标坐标互为相反数.
关于原点对称的两点横、纵坐标均互为相反数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11. 实数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是( )
实数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是( )
 实数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是( )
实数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是( )| A. | ac>bc | B. | |a-b|=a-b | C. | -a-c>-b-c | D. | -a<-b<c |
1.如图所示,图①中的多边形(边数为12)是由等边三角形“扩展”而来的,图②中的多边形是由正方形“扩展”而来的,…,依此类推,则由正n边形“扩展”而来的多边形的边数为( )
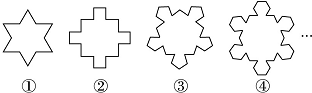

| A. | n(n-1) | B. | n(n+1) | C. | (n+1)(n-1) | D. | n2+2 |
6.在锐角△ABC中,|sinA-$\frac{\sqrt{3}}{2}$|+(cosB-$\frac{\sqrt{2}}{2}$)2=0,则∠C的度数是( )
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
 如图,已知一个等腰三角形和一条线段,以这条线段为边画三角形,使之与已知等腰三角形相似,你能画出几个形状不同的三角形?
如图,已知一个等腰三角形和一条线段,以这条线段为边画三角形,使之与已知等腰三角形相似,你能画出几个形状不同的三角形?
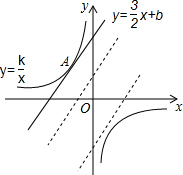 如图,已知双曲线y=$\frac{k}{x}$与直线y=$\frac{3}{2}$x+b.
如图,已知双曲线y=$\frac{k}{x}$与直线y=$\frac{3}{2}$x+b.