题目内容
已知a、b互为相反数,c、d互为倒数,求
+(a+b)2014+[-(-cd)]2014的值.
| b |
| a |
考点:代数式求值,相反数,倒数
专题:
分析:利用相反数以及倒数的定义得出a+b=0,cd=1,进而求出即可.
解答:解:∵a、b互为相反数,c、d互为倒数,
∴a+b=0,cd=1,
∴
+(a+b)2014+[-(-cd)]2014
=-1+0+1
=0.
∴a+b=0,cd=1,
∴
| b |
| a |
=-1+0+1
=0.
点评:此题主要考查了代数式求值,得出a+b=0,cd=1是解题关键.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
在下列方程中,一元二次方程的个数是( )
①3x2+7=0;②ax2+bx+c=0;③(x-2)(x+5)=x2-1;④3x2-
=0.
①3x2+7=0;②ax2+bx+c=0;③(x-2)(x+5)=x2-1;④3x2-
| 5 |
| x |
| A、1个 | B、2个 | C、3个 | D、4个 |
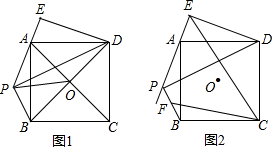
已知线段m、n(m>n),用直尺和圆规作等腰△ABC,使AB=AC=m,BC=n,再分别以AB、AC为边向形外作等边△ABD和等边△ACE,连接BE、CD,则( )
| A、BE>CD |
| B、BE=CD |
| C、BE<CD |
| D、BE≤CD |
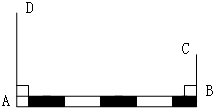 如图,铁路上A、B两点(看作直线上的两点)相距40千米,C、D为两个村庄(看作两个点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=24千米,BC=16千米,求两个村庄的距离.
如图,铁路上A、B两点(看作直线上的两点)相距40千米,C、D为两个村庄(看作两个点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=24千米,BC=16千米,求两个村庄的距离. 已知:如图,点A、B、C、D在一条直线上,AC=DB,AE=DF,BE=CF.
已知:如图,点A、B、C、D在一条直线上,AC=DB,AE=DF,BE=CF. 如图是由大小相同的棱长为2cm的小正方体搭成的几何体,
如图是由大小相同的棱长为2cm的小正方体搭成的几何体,