题目内容
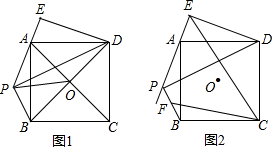
如图,O是□ABCD两对角线的交点,线段OB绕着点O顺时针旋转α°(0≤α≤360),B点的对应点为P点,DE⊥PA于E点.
(1)填空:如图1,∠EPD= °,
= ;
(2)如图2,若F为PB的中点,连接CF、CE,求∠ECF的度数;
(3)若AB=2,当线段OB绕着O点旋转时,则线段CE长度的最大值为 .
(1)填空:如图1,∠EPD=
| PB |
| AE |
(2)如图2,若F为PB的中点,连接CF、CE,求∠ECF的度数;
(3)若AB=2,当线段OB绕着O点旋转时,则线段CE长度的最大值为

考点:四边形综合题,四点共圆,线段的性质:两点之间线段最短,勾股定理,三角形中位线定理,圆周角定理,圆内接四边形的性质,相似三角形的判定与性质
专题:综合题
分析:(1)如图1,易证P、B、D、A四点共圆,根据圆周角定理可得∠APD=∠ABD=45°,∠BPD=∠BAD=90°,根据圆内接四边形的性质可得∠EAD=∠PBD,进而可证到△PBD∽△EAD,然后运用相似三角形的性质就可求出
的值.
(2)连接OF,如图2,根据三角形中位线定理可得OF∥DP,OF=
PD.进而可证到
=
=
,∠FOC=∠EDC,从而有△EDC∽△FOC,则有∠DCE=∠OCF,就可得到∠ECF的度数.
(3)取AD的中点Q,连接EQ,如图3,易证点E运动的路径是以点Q为圆心,QA为半径的圆,然后根据两点之间线段最短即可求出线段CE长度的最大值.
| PB |
| AE |
(2)连接OF,如图2,根据三角形中位线定理可得OF∥DP,OF=
| 1 |
| 2 |
| ED |
| OF |
| 2 |
| DC |
| OC |
(3)取AD的中点Q,连接EQ,如图3,易证点E运动的路径是以点Q为圆心,QA为半径的圆,然后根据两点之间线段最短即可求出线段CE长度的最大值.
解答:解:(1)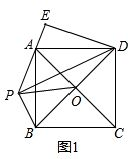 如图1,
如图1,
∵四边形ABCD是正方形,
∴OA=OB=OC=OD,∠ABD=∠ADB=45°,BD=
AD.
∵OP=OB,
∴OP=OB=OA=OD
∴P、B、D、A四点共圆,
∴∠APD=∠ABD=45°,∠BPD=∠BAD=90°,∠EAD=∠PBD.
∵DE⊥PA即∠AED=90°,
∴∠BPD=∠AED=90°,
∵∠EAD=∠PBD,∠BPD=∠AED,
∴△PBD∽△EAD,
∴
=
=
.
故答案分别为:45、
.
(2)连接OP,如图2.
∵OB=OD,FB=FP,
∴OF∥DP,OF=
PD.
∴∠PDB=∠FOB.
∵△PBD∽△EAD,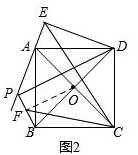
∴∠PDB=∠EDA,
∴∠FOB=∠EDA.
在Rt△PED中,
sin∠EPD=
=sin45°=
,
∴PD=
ED,
∴2OF=
ED,
∴ED=
OF.
∵四边形ABCD是正方形,
∴∠BOC=∠ADC=90°,∠DCA=45°,DC=
OC.
∴
=
=
,∠EDC=∠FOC.
∴△EDC∽△FOC,
∴∠DCE=∠OCF,
∴∠DCA=∠ECF=45°.
∴∠ECF的度数为45°.
(3)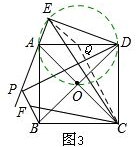 取AD的中点Q,连接EQ、QC,如图3.
取AD的中点Q,连接EQ、QC,如图3.
∵∠AED=90°,点Q为AD的中点,
∴EQ=AQ=DQ,
∴点E在以点Q为圆心,QA为半径的圆上,
∴QE=QD=
AD=1.
在Rt△QDC中,
QC=
=
=
,
∴EC≤QC+QE=
+1,
∴当E、Q、C三点共线时,EC取到最大值,最大值为
+1.
故答案为:
+1.
 如图1,
如图1,∵四边形ABCD是正方形,
∴OA=OB=OC=OD,∠ABD=∠ADB=45°,BD=
| 2 |
∵OP=OB,
∴OP=OB=OA=OD
∴P、B、D、A四点共圆,
∴∠APD=∠ABD=45°,∠BPD=∠BAD=90°,∠EAD=∠PBD.
∵DE⊥PA即∠AED=90°,
∴∠BPD=∠AED=90°,
∵∠EAD=∠PBD,∠BPD=∠AED,
∴△PBD∽△EAD,
∴
| PB |
| EA |
| BD |
| AD |
| 2 |
故答案分别为:45、
| 2 |
(2)连接OP,如图2.
∵OB=OD,FB=FP,
∴OF∥DP,OF=
| 1 |
| 2 |
∴∠PDB=∠FOB.
∵△PBD∽△EAD,

∴∠PDB=∠EDA,
∴∠FOB=∠EDA.
在Rt△PED中,
sin∠EPD=
| ED |
| PD |
| ||
| 2 |
∴PD=
| 2 |
∴2OF=
| 2 |
∴ED=
| 2 |
∵四边形ABCD是正方形,
∴∠BOC=∠ADC=90°,∠DCA=45°,DC=
| 2 |
∴
| ED |
| OF |
| 2 |
| DC |
| OC |
∴△EDC∽△FOC,
∴∠DCE=∠OCF,
∴∠DCA=∠ECF=45°.
∴∠ECF的度数为45°.
(3)
 取AD的中点Q,连接EQ、QC,如图3.
取AD的中点Q,连接EQ、QC,如图3.∵∠AED=90°,点Q为AD的中点,
∴EQ=AQ=DQ,
∴点E在以点Q为圆心,QA为半径的圆上,
∴QE=QD=
| 1 |
| 2 |
在Rt△QDC中,
QC=
| QD2+DC2 |
| 12+22 |
| 5 |
∴EC≤QC+QE=
| 5 |
∴当E、Q、C三点共线时,EC取到最大值,最大值为
| 5 |
故答案为:
| 5 |
点评:本题考查了正方形的性质、四点共圆的判定、三角形的中位线定理、勾股定理、圆周角定理、圆内接四边形的性质、相似三角形判定与性质、两点之间线段最短等知识,综合性比较强,有一定的难度.证明P、B、D、A四点共圆是解决第(1)小题的关键,证明△EDC∽△FOC是解决第(2)小题的关键,确点E的路径并运用两点之间线段最短则是解决第(3)小题的关键.

练习册系列答案
相关题目
 如图所示,点B、C在∠BAC的两边上,点D、E在∠BAC两边的反向延长线上,且DE∥BC.若AB=5,AC=6,AD=2,求AE的长.
如图所示,点B、C在∠BAC的两边上,点D、E在∠BAC两边的反向延长线上,且DE∥BC.若AB=5,AC=6,AD=2,求AE的长.