题目内容
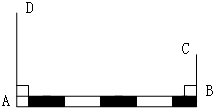 如图,铁路上A、B两点(看作直线上的两点)相距40千米,C、D为两个村庄(看作两个点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=24千米,BC=16千米,求两个村庄的距离.
如图,铁路上A、B两点(看作直线上的两点)相距40千米,C、D为两个村庄(看作两个点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=24千米,BC=16千米,求两个村庄的距离.考点:勾股定理的应用
专题:
分析:连接CD,作CE⊥AD于点E,根据AD⊥AB,BC⊥AB得到BC=AE,CE=AB,从而得到DE=AD-AE=24-16=8千米,利用勾股定理求得CD两地之间的距离.
解答: 解:如图,连接CD,作CE⊥AD于点E,
解:如图,连接CD,作CE⊥AD于点E,
∵AD⊥AB,BC⊥AB,
∴BC=AE,CE=AB,
∴DE=AD-AE=24-16=8千米,
∴CD=
=
=8
千米,
∴两个村庄相距8
千米.
 解:如图,连接CD,作CE⊥AD于点E,
解:如图,连接CD,作CE⊥AD于点E,∵AD⊥AB,BC⊥AB,
∴BC=AE,CE=AB,
∴DE=AD-AE=24-16=8千米,
∴CD=
| DE2-CE2 |
| 82+402 |
| 26 |
∴两个村庄相距8
| 26 |
点评:考查了勾股定理的应用,解题的关键是从实际问题中抽象出直角三角形,难度不大.

练习册系列答案
相关题目
 如图,
如图,
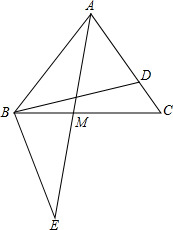 如图,在等边△ABC中,∠BDC+∠CBE=180°,BD=BE,AD:DC=3:1,求BM:CM.
如图,在等边△ABC中,∠BDC+∠CBE=180°,BD=BE,AD:DC=3:1,求BM:CM. 如图,△ACE≌△DBF,∠E=∠F,AD=10,BC=4.
如图,△ACE≌△DBF,∠E=∠F,AD=10,BC=4.