题目内容
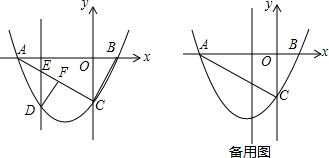
20.如图,抛物线y=$\frac{1}{2}$x2+$\frac{3}{2}$x-2与x轴交于A、B两点,(A点在B点左边),与y轴交于点C,连接AC、BC.(1)求点A、B、C的坐标;
(2)M为该抛物线对称轴上一点,是否存在以AC为斜边的直角三角形MAC?若存在,求点M的坐标,并求三角形MAC的面积;若不存在,请说明理由;
(3)D为第三象限抛物线上一动点,直线DE∥y轴交线段AC于E点,过D点作DF∥CB交AC于F点,求△DEF周长的最大值和此时点F的坐标.
分析 (1)令y=0求A、B两点横坐标,令x=0求C点纵坐标;
(2)求得对称轴,然后设M(-$\frac{3}{2}$,n),根据勾股定理列出关于n的方程,解方程即可求得M的坐标,然后求得直线AB与对称轴的交点坐标,根据三角形MAC的面积等于两个三角形面积的和求得即可;
(3)先求得△ACO的周长,然后求得△DEF∽△ACO,然后利用相似三角形的周长比等于对应边的比来列式求解.
解答 解:(1)令y=0,则$\frac{1}{2}$x2+$\frac{3}{2}$x-2=0,解得x1=-4,x2=1.
令x=0,则y=-2,
所以A、B、C的坐标分别是A(-4,0)、B(1,0)、C(0,-2);
(2)∵y=$\frac{1}{2}$x2+$\frac{3}{2}$x-2=$\frac{1}{2}$(x+$\frac{3}{2}$)2-$\frac{25}{8}$,
∴对称轴为x=-$\frac{3}{2}$,
设M(-$\frac{3}{2}$,n),
∵A(-4,0)、C(0,-2);
∴MA2=(-$\frac{3}{2}$+4)2+n2=$\frac{25}{4}$+n2,MC2=(-$\frac{3}{2}$)2+(n+2)2=n2+4n+$\frac{25}{4}$,AC2=42+22=20,
∵△MAC是以AC为斜边的直角三角形,
∴MA2+MC2=AC2,即$\frac{25}{4}$+n2+n2+4n+$\frac{25}{4}$=20,
解得n=-1±$\frac{\sqrt{19}}{2}$,
∴M(-$\frac{3}{2}$,-1+$\frac{\sqrt{19}}{2}$)或(-$\frac{3}{2}$,-1-$\frac{\sqrt{19}}{2}$);
由A(-4,0)、C(0,-2)可知直线AC的解析式为y=-$\frac{1}{2}$x-2,
把x=-$\frac{3}{2}$代入得,y=-$\frac{5}{4}$,
∴直线AB与对称轴的交点为(-$\frac{3}{2}$,-$\frac{5}{4}$),
当M(-$\frac{3}{2}$,-1+$\frac{\sqrt{19}}{2}$)时,S△MAC=$\frac{1}{2}$(-1+$\frac{\sqrt{19}}{2}$+$\frac{5}{4}$)×4=$\frac{1+2\sqrt{19}}{2}$;
当M(-$\frac{3}{2}$,-1-$\frac{\sqrt{19}}{2}$)时,S△MAC=$\frac{1}{2}$(-$\frac{5}{4}$+1+$\frac{\sqrt{19}}{2}$)×4=$\frac{2\sqrt{19}-1}{2}$;
(3)∵直线AC的解析式为y=-$\frac{1}{2}$x-2,
设点D的横坐标为t,
∴D(t,$\frac{1}{2}$t2+$\frac{3}{2}$t-2),E(t,-$\frac{1}{2}$t-2),
∴DE=(-$\frac{1}{2}$t-2)-($\frac{1}{2}$t2+$\frac{3}{2}$t-2)=-$\frac{1}{2}$t2-2t,
∵A(-4,0)、B(1,0)、C(0,-2);
∴OA=4,OC=2,OB=1,
∴AC=$\sqrt{20}$,BC=$\sqrt{5}$,AB=5,
∵AC2+BC2=AB2=25,
∴∠ACB=90°,
∵DF∥CB,
∴∠DFE=90°,
∵DE∥y轴,
∴∠ACO=∠DEF,
∵∠DFE=∠AOC=90°,
∴△DEF∽△ACO,
∴$\frac{△DEF周长}{△ACO周长}$=$\frac{DE}{AC}$=$\frac{-\frac{1}{2}{t}^{2}-2t}{\sqrt{20}}$,
∵△ACO的周长=OA+OC+AC=4+2+$\sqrt{20}$=6+2$\sqrt{5}$,
∴△DEF的周长=$\frac{6+2\sqrt{5}}{2\sqrt{5}}$(-$\frac{1}{2}$t2-2t)=-$\frac{6+2\sqrt{5}}{4\sqrt{5}}$(t+2)2+$\frac{6\sqrt{5}+10}{5}$,
∴当t=-2时,△DEF周长的最大值=$\frac{6\sqrt{5}+10}{5}$,此时D(-2,-3),
∵直线AC的解析式为y=-$\frac{1}{2}$x-2,
∴设直线DF的解析式为y=2x+b,
把D(-2,-3)代入得,-3=-4+b,
∴b=1,
∴线DF的解析式为y=2x+1
解$\left\{\begin{array}{l}{y=2x+1}\\{y=-\frac{1}{2}x-2}\end{array}\right.$得$\left\{\begin{array}{l}{x=-\frac{6}{5}}\\{y=-\frac{7}{5}}\end{array}\right.$,
∴F(-$\frac{6}{5}$,-$\frac{7}{5}$).
点评 此题主要考查了二次函数图象上点的坐标特征、相似三角形的判断和性质、等勾股定理的应用以及直角三角形的判定等;后面两个小题中,利用几何知识来解是比较简便快捷的方式,体现了数形结合思想的合理应用.

 阅读快车系列答案
阅读快车系列答案 函数y=x2+2x-3的图象如图所示,当x=m时,y<0,则m的值可能是( )
函数y=x2+2x-3的图象如图所示,当x=m时,y<0,则m的值可能是( )| A. | -4 | B. | $\frac{1}{2}$ | C. | 2 | D. | 3 |
 如图,Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB,垂足为点D,则AD的长为( )
如图,Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB,垂足为点D,则AD的长为( )| A. | $\frac{25}{4}$ | B. | 6 | C. | $\frac{24}{5}$ | D. | 4 |
| A. | -3 | B. | 3 | C. | ±3 | D. | 0 |
 △ABC三个顶点A、B、C的坐标分别为A(2,-1)、B(1,-3)、C(4,-2).
△ABC三个顶点A、B、C的坐标分别为A(2,-1)、B(1,-3)、C(4,-2).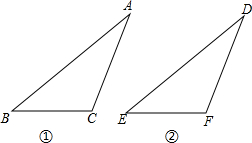 根据要求设计一种方案(包括画出相应的图形.指出需要测量的线段等).
根据要求设计一种方案(包括画出相应的图形.指出需要测量的线段等). 画图并计算:已知直线AB上有一点C,M是线段AC的中点,若BC=4cm,AB=10cm,求AM的长.
画图并计算:已知直线AB上有一点C,M是线段AC的中点,若BC=4cm,AB=10cm,求AM的长.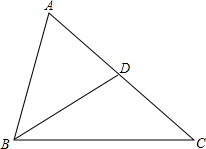 如图,∠ABD=∠C,AD=2,AC=8,求AB.
如图,∠ABD=∠C,AD=2,AC=8,求AB.