题目内容
3.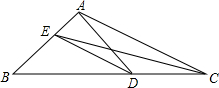 如图,在△ABC中,点D是BC上的一点,已知∠DAC=30°,∠DAB=75°,CE平分∠ACB交AB于点E,连接DE,则∠DEC=( )
如图,在△ABC中,点D是BC上的一点,已知∠DAC=30°,∠DAB=75°,CE平分∠ACB交AB于点E,连接DE,则∠DEC=( )| A. | 10° | B. | 15° | C. | 20° | D. | 25° |
分析 过点E作EM⊥AC于M,EN⊥AD于N,EF⊥BC于H,如图,先计算出∠EAM=75°,则AE平分∠EAD,根据角平分线的性质得EM=EN,再由CE平分∠ACB得到EM=EH,则EN=EH,于是根据角平分线定理的逆定理可判断DE平分∠ADB,则∠1=$\frac{1}{2}$∠ADB,根据三角形外角性质得∠1=∠DEC+∠2,即∠1=∠DEC+$\frac{1}{2}$∠ACB,∠ADB=∠DAC+∠ACB,所以∠DEC=$\frac{1}{2}$∠DAC=15°.
解答 解:过点E作EM⊥AC于M,EN⊥AD于N,EF⊥BC于H,如图,
∵∠DAC=30°,∠DAB=75°,
∴∠EAM=75°,
∴AE平分∠EAD,
∴EM=EN,
∵CE平分∠ACB,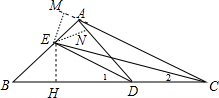
∴EM=EH,
∴EN=EH,
∴DE平分∠ADB,
∴∠1=$\frac{1}{2}$∠ADB,
∵∠1=∠DEC+∠2,
而∠2=$\frac{1}{2}$∠ACB,
∴∠1=∠DEC+$\frac{1}{2}$∠ACB,
而∠ADB=∠DAC+∠ACB,
∴∠DEC=$\frac{1}{2}$∠DAC=$\frac{1}{2}$×30°=15°.
故选B.
点评 本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.解决本题的关键是运用角平分线定理的逆定理证明DE平分∠ADB.

练习册系列答案
相关题目
15. 函数y=x2+2x-3的图象如图所示,当x=m时,y<0,则m的值可能是( )
函数y=x2+2x-3的图象如图所示,当x=m时,y<0,则m的值可能是( )
 函数y=x2+2x-3的图象如图所示,当x=m时,y<0,则m的值可能是( )
函数y=x2+2x-3的图象如图所示,当x=m时,y<0,则m的值可能是( )| A. | -4 | B. | $\frac{1}{2}$ | C. | 2 | D. | 3 |
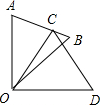 如图,△COD是△AOB绕点O顺时针方向旋转40°后所得的图形,点C恰好在AB上,∠AOD=90°,求∠A和∠B的度数.
如图,△COD是△AOB绕点O顺时针方向旋转40°后所得的图形,点C恰好在AB上,∠AOD=90°,求∠A和∠B的度数. 根据要求设计一种方案(包括画出相应的图形.指出需要测量的线段等).
根据要求设计一种方案(包括画出相应的图形.指出需要测量的线段等). 已知x轴上两点A(-1,0)、B(4,0).
已知x轴上两点A(-1,0)、B(4,0). 画图并计算:已知直线AB上有一点C,M是线段AC的中点,若BC=4cm,AB=10cm,求AM的长.
画图并计算:已知直线AB上有一点C,M是线段AC的中点,若BC=4cm,AB=10cm,求AM的长.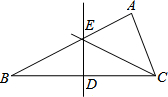 如图,在Rt△ABC中,∠A=90°,BC边的垂直平分线交BC于点D,交AB与E,若CE平分∠ACB,EC=5,ED=3,则AB的长是8.
如图,在Rt△ABC中,∠A=90°,BC边的垂直平分线交BC于点D,交AB与E,若CE平分∠ACB,EC=5,ED=3,则AB的长是8.