题目内容
15．抛物线y=（x+1）2+2的顶点是（ ）| A． | （1，2） | B． | （-1，2） | C． | （-1，-2） | D． | （1，-2） |
分析 由抛物线解析式可求得顶点坐标．
解答 解：
∵y=（x+1）2+2，
∴顶点坐标为（-1，2），
故选B．
点评 本题主要考查二次函数的性质，掌握二次函数的顶点式是解题的关键，即在y=a（x-h）2+k中，对称轴为x=h，顶点坐标为（h，k）．
练习册系列答案
名校课堂系列答案
相关题目
6．$\frac{1}{4}$的算术平方根是（ ）
| A． | ±$\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{1}{16}$ |
3．下列四个标志中，是轴对称图形的是图（ ）
| A． |  | B． |  | C． |  | D． |  |
10．若点（-4，y1），（2，y2）都在y=-$\frac{1}{3}$x+b的图象上，则y1与y2的大小关系是（ ）
| A． | y1＞y2 | B． | y1=y2 | C． | y1＜y2 | D． | 无法确定 |
20．不等式组$\left\{\begin{array}{l}{x+2＞0}\\{2x-1≤0}\end{array}\right.$的所有整数解是（ ）
| A． | -1、0 | B． | -2、-1 | C． | 0、1 | D． | -2、-1 |
7．若点M（m，n）（mn≠0）在二次函数y=ax2（a≠0）图象上，则下列坐标表示的点也在该抛物线图象上的是（ ）
| A． | （-m，n） | B． | （n，m） | C． | （m2，n2） | D． | （m，-n） |
4．
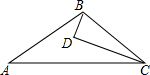如图，D为△ABC内一点，CD平分∠ACB，BD⊥CD，∠A=∠ABD，若AC=5，BC=3，则BD的长为（ ）
如图，D为△ABC内一点，CD平分∠ACB，BD⊥CD，∠A=∠ABD，若AC=5，BC=3，则BD的长为（ ）| A． | 1 | B． | 1.5 | C． | 2$\sqrt{2}$ | D． | 4 |
5．对于a＞b＞c＞0，m＞n＞0（m、n是正整数），成立的关系式是（ ）
| A． | ambn＞bncm＞cnam | B． | ambn＞cnam＞bncm | C． | amcn＞ambn＞bncm | D． | bnam＞cnam＞ambn |