题目内容
2.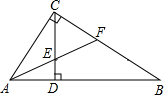 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AF平分∠CAB,交CD于E,交BC于F,若AF=BF,求证:△CEF是等边三角形.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AF平分∠CAB,交CD于E,交BC于F,若AF=BF,求证:△CEF是等边三角形.
分析 在△ABC中,AF平分∠CAB、AF=BF求得∠B=∠2=∠1=60°,根据外角性质可得∠4=60°,在RT△ADE中可得∠3=∠5=60°,进而可知∠4=∠5=60°,得证.
解答 证明:如图,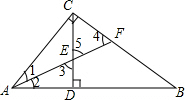
∵AF是∠BAC的平分线,
∴∠CAB=2∠1=2∠2,
∵AF=BF,
∴∠2=∠B,
∵∠ACB=90°,
∴∠B+∠CAB=90°,即∠B+2∠1=∠B+2∠2=90°,
∴∠B=∠1=∠2=30°,
∵∠4是△ABF的外角,
∴∠4=∠2+∠B=60°,
∵CD是AB边上的高,
∴∠2+∠3=90°,
∴∠3=60°,
∵∠5=∠3,
∴∠4=∠5=60°,
∴△CEF是等边三角形.
点评 本题考查了等边三角形的判定、等腰三角形的性质、角平分线的定义、直角三角形两锐角互余的性质,利用阿拉伯数字加弧线表示角更简单明了.

练习册系列答案
相关题目
14. 如图,矩形ABCD的边AB在x轴上,AB的中点与原点O重合,AB=2,AD=1,点Q的坐标为(0,2).点P(x,0)在边AB上运动,若过点Q、P的直线将矩形ABCD的周长分成2:1两部分,则x的值为( )
如图,矩形ABCD的边AB在x轴上,AB的中点与原点O重合,AB=2,AD=1,点Q的坐标为(0,2).点P(x,0)在边AB上运动,若过点Q、P的直线将矩形ABCD的周长分成2:1两部分,则x的值为( )
 如图,矩形ABCD的边AB在x轴上,AB的中点与原点O重合,AB=2,AD=1,点Q的坐标为(0,2).点P(x,0)在边AB上运动,若过点Q、P的直线将矩形ABCD的周长分成2:1两部分,则x的值为( )
如图,矩形ABCD的边AB在x轴上,AB的中点与原点O重合,AB=2,AD=1,点Q的坐标为(0,2).点P(x,0)在边AB上运动,若过点Q、P的直线将矩形ABCD的周长分成2:1两部分,则x的值为( )| A. | $\frac{1}{2}$或$-\frac{1}{2}$ | B. | $\frac{1}{3}$或$-\frac{1}{3}$ | C. | $\frac{3}{4}$或$-\frac{3}{4}$ | D. | $\frac{2}{3}$或$-\frac{2}{3}$ |
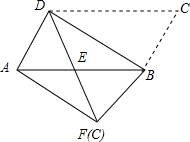 如图,将平行四边形ABCD沿对角线BD进行折叠,折叠后点C落在点F处,DF交AB于点E.
如图,将平行四边形ABCD沿对角线BD进行折叠,折叠后点C落在点F处,DF交AB于点E. 如图,△ABC中,∠ACB=90°,AC=BC,P是△ABC内一点,且PA=6,PB=2,PC=4,求证:∠BPC=135°.
如图,△ABC中,∠ACB=90°,AC=BC,P是△ABC内一点,且PA=6,PB=2,PC=4,求证:∠BPC=135°.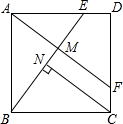 如图,四边形ABCD是正方形,E,F分别在AD,BC上,且DE=CF,连结AF,BE交于点M,过C作CN⊥BE于点N.求证:AM+MN=CN.
如图,四边形ABCD是正方形,E,F分别在AD,BC上,且DE=CF,连结AF,BE交于点M,过C作CN⊥BE于点N.求证:AM+MN=CN.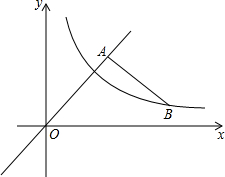 如图,已知A为直线y=x上一点,过A作BA⊥OA交双曲线y=$\frac{k}{x}$于B,若OA2-AB2=8,求k的值.
如图,已知A为直线y=x上一点,过A作BA⊥OA交双曲线y=$\frac{k}{x}$于B,若OA2-AB2=8,求k的值.