题目内容

6．如图，AD是△ABC的中线，E、F分别是AB、AC的中点，求证：四边形AEDF是平行四边形．

分析 利用三角形中位线定理推知AE∥FD，AF∥ED，则“有两组对边相互平行的四边形为平行四边形”证得结论．

解答 证明：∵AD是△ABC的中线，
∴点D是BC的中点，
又∵E是AB的中点，
∴ED是△ABC的中位线，
∴ED∥AC，则ED∥AF．
同理，AF∥ED，
∴四边形AEDF四边形AEDF．

点评 此题主要考查了平行四边形的判定以及三角形的中位线的性质，正确掌握平行四边形的判定方法是解题关键．

练习册系列答案
相关题目
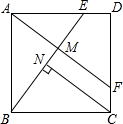16．已知抛物线经过点（2，3），且顶点坐标为（1，1），求这条抛物线的解析式．
17．如图，四边形ABCD是正方形，E，F分别在AD，BC上，且DE=CF，连结AF，BE交于点M，过C作CN⊥BE于点N．求证：AM+MN=CN．
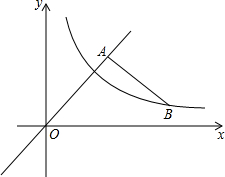14．如图，已知A为直线y=x上一点，过A作BA⊥OA交双曲线y=$\frac{k}{x}$于B，若OA2-AB2=8，求k的值．
1．在方程组①$\left\{\begin{array}{l}{2x+y=3}\\{y=2x-1}\end{array}\right.$；②$\left\{\begin{array}{l}{x=3}\\{y-x=0}\end{array}\right.$；③$\left\{\begin{array}{l}{xy=2}\\{x=4}\end{array}\right.$；④$\left\{\begin{array}{l}{x+{x}^{2}=5}\\{y-1=x}\end{array}\right.$；⑤$\left\{\begin{array}{l}{\frac{1}{x}+y=3}\\{\frac{1}{x}-y=1}\end{array}\right.$；⑥$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$中，属于二元一次方程组的有（　　）
A．1个B．2个C．3个D．4个
11．已知x=$\sqrt{2015}$-1，求x2+2x+5的值．
18．如图所示，这三种卡片的数量分别有3张，2张，1张，请你用它们拼出一些长方形或正方形，要求每种卡片都要用到，卡片之间不重叠，并用两种不同的方式计算它的面积．
15．计算$\frac{1}{1+\root{4}{10}}+\frac{1}{1-\root{4}{10}}+\frac{2}{1+\sqrt{10}}$的值．
18．如图所示，在边长为2的正方形ABCD的边上有一个动点P，从点A出发沿折线ABCD移动一周后，回到A点．设点A移动的路程为x，△PAC的面积为y，求函数y的解析式．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网