题目内容
12. 如图,AB为⊙O的直径,PA为⊙O的切线,PB交⊙O于点C,PD平分∠APB交AB于点D,交AC于点E.
如图,AB为⊙O的直径,PA为⊙O的切线,PB交⊙O于点C,PD平分∠APB交AB于点D,交AC于点E.(1)求证:AE=AD;
(2)若PE=3,DE=2,求cos∠PEC的值.
分析 (1)由切线的性质和直径所对的圆周角为90°得:∠PAB=∠ACB=90°,再由同角的余角相等和外角定理得:∠EDA=∠DEA,根据等角对等边得:AE=AD;
(2)作辅助线,利用同角的三角函数列式求AD的长,根据(1)中的结论:AD=AE,得:∠PEC=∠AED=∠ADF,根据三角函数定义可得结论.
解答 证明:(1)∵PA为⊙O的切线,AB是⊙O的直径,
∴∠PAB=90°,∠ACB=90°
∴∠PAC+∠CAB=90°,∠CAB+∠B=90°
∴∠PAC=∠B,
∵∠EDA=∠B+∠BPD,∠DEA=∠PAC+∠APD,
∵∠BPD=∠APD,
∴∠EDA=∠DEA,
∴AE=AD;
(2)过A作AF⊥ED于F,
∵AE=AD,
∴EF=FD=$\frac{1}{2}$ED=$\frac{1}{2}$×2=1,
∵∠AFD=∠PAD=90°,
∴cos∠ADF=$\frac{DF}{AD}$=$\frac{AD}{PD}$,
∴$\frac{1}{AD}=\frac{AD}{3+2}$,
∴AD=$±\sqrt{5}$,
∵AD>0,
∴AD=-$\sqrt{5}$不符合题意,舍去,
∴AD=$\sqrt{5}$,
∵∠PEC=∠AED=∠ADF,
∴cos∠PEC=cos∠ADF=$\frac{1}{\sqrt{5}}$=$\frac{\sqrt{5}}{5}$.
点评 本题考查了切线的性质、三角函数的定义,熟练运用同角或等角的三角函数列式,求线段的长,或运用三角形相似解决问题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
17.点P(n+3,n+1)在平面直角坐标系的y轴上,则点P的坐标为( )
| A. | (0,2) | B. | (2,0) | C. | (0,-2) | D. | (0,-4) |
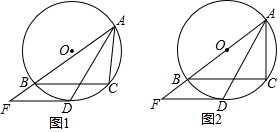
 如图所示,四边形ABCD为平行四边形,CE平分∠BCD,交AB边于点E,若AD=6,AB=8,则线段AE的长为2.
如图所示,四边形ABCD为平行四边形,CE平分∠BCD,交AB边于点E,若AD=6,AB=8,则线段AE的长为2.