题目内容
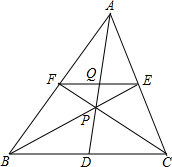 已知.如图,P为△ABC中线AD上一点,AP:PD=2:1,延长BP、CP分别交AC、AB于E、F,EF交AD于Q.
已知.如图,P为△ABC中线AD上一点,AP:PD=2:1,延长BP、CP分别交AC、AB于E、F,EF交AD于Q.(1)FQ=EQ;
(2)FP:PC=EC:AE;
(3)FQ:BD=PQ:PD;
(4)S△FPQ:S△DCP=S△AEF:S△ABC,
上述结论中,正确的有
考点:相似三角形的判定与性质
专题:
分析:首先延长PD到M,使DM=PD,连接BM、CM,易得四边形BPCM是平行四边形,然后由平行线分线段成比例定理,证得AE:AC=AP:AM,AF:AB=AP:AM,继而证得EF∥BC;然后由相似三角形的性质,证得结论.
解答:解:延长PD到M,使DM=PD,连接BM、CM,
∵AD是中线,
∴BD=CD,
∴四边形BPCM是平行四边形,
∴BP∥MC,CP∥BM,
即PE∥MC,PF∥BM,
∴AE:AC=AP:AM,AF:AB=AP:AM,
∴AF:AB=AE:AC,
∴EF∥BC;
 ∴△AFQ∽△ABD,△AEQ∽△ACD,
∴△AFQ∽△ABD,△AEQ∽△ACD,
∴FQ:BD=EQ:CD,
∴FQ=EQ,故(1)正确;
∵△△PEF∽△PBC,△AEF∽△ACB,
∴PF:PC=EF:BC,EF:BC=AE:AC,
∴PF:PC=AE:AC,故(2)错误;
∵△PFQ∽△PCD,
∴FQ:CD=PQ:PD,
∴FQ:BD=PQ:PD;故(3)正确;
∵S△FPQ:S△DCP=(
)2=(
)2=(
)2,S△AEF:S△ABC=(
)2,
∴S△FPQ:S△DCP=S△AEF:S△ABC.故(4)正确.
故答案为:(1)(3)(4).
∵AD是中线,
∴BD=CD,
∴四边形BPCM是平行四边形,
∴BP∥MC,CP∥BM,
即PE∥MC,PF∥BM,
∴AE:AC=AP:AM,AF:AB=AP:AM,
∴AF:AB=AE:AC,
∴EF∥BC;
 ∴△AFQ∽△ABD,△AEQ∽△ACD,
∴△AFQ∽△ABD,△AEQ∽△ACD,∴FQ:BD=EQ:CD,
∴FQ=EQ,故(1)正确;
∵△△PEF∽△PBC,△AEF∽△ACB,
∴PF:PC=EF:BC,EF:BC=AE:AC,
∴PF:PC=AE:AC,故(2)错误;
∵△PFQ∽△PCD,
∴FQ:CD=PQ:PD,
∴FQ:BD=PQ:PD;故(3)正确;
∵S△FPQ:S△DCP=(
| FQ |
| CD |
| FQ |
| BD |
| AF |
| AB |
| AF |
| AB |
∴S△FPQ:S△DCP=S△AEF:S△ABC.故(4)正确.
故答案为:(1)(3)(4).
点评:此题考查了相似三角形的判定与性质、平行线分线段成比例定理以及平行四边形的性质与判定.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
 如图,已知
如图,已知
 如图,点D是△ABC的边BC上任意一点,点E、F分别是线段AD、CE的中点,且△ABC的面积为18cm2,则△BEF的面积=
如图,点D是△ABC的边BC上任意一点,点E、F分别是线段AD、CE的中点,且△ABC的面积为18cm2,则△BEF的面积=