题目内容

抛物线y=x2-4x+5的顶点坐标是（　　）
A、（2，1）
B、（-2，1）
C、（2，5）
D、（-2，5）
考点：二次函数的性质
专题：
分析：已知抛物线的解析式是一般式，用配方法转化为顶点式，根据顶点式的坐标特点，直接写出顶点坐标．
解答：解：∵y=x2-4x+5=x2-4x+4-4+5=（x-2）2+1，
∴抛物线y=x2-4x+5的顶点坐标是（2，1）．
故选A．
点评：此题考查了二次函数的性质，二次函数y=a（x-h）2+k的顶点坐标为（h，k），对称轴为x=h，此题还考查了配方法求顶点式．
练习册系列答案
相关题目
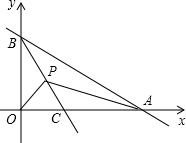如图，A、B分别为x轴和y轴正半轴上的点．OA、OB的长分别是x2-14x+48=0的两根（OA＞OB），直线BC平分∠ABO交x轴于C点，P为BC上一动点，P点以每秒1个单位的速度从B点开始沿BC方向向终点C移动
（1）设△APB和△OPB的面积为S1，S2，则S1：S2=
 
．
（2）P点移动时间为t，当t=
 
时△OPC是等腰三角形．
cosA=
3
2
（A为锐角），则∠A的度数为（　　）
A、60°B、30°
C、45°D、30°或60°
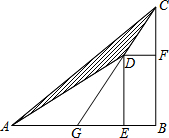如图，D为△ABC内部一点，E、F两点分别在AB、BC上，且四边形DEBF为矩形，直线CD交AB于G点．若CF=6，BF=9，AG=8，则△ADC的面积为何？（　　）
A、16B、24C、36D、54
下列真命题中逆命题也是真命题的是（　　）
A、对顶角相等
B、全等三角形对应角相等
C、全等三角形对应边相等
D、等边三角形是锐角三角形
解方程：
-2
x-3
+1=
2
x
．
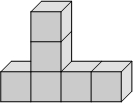如图是由一些棱长都为1cm的小正方体组合成的简单几何体．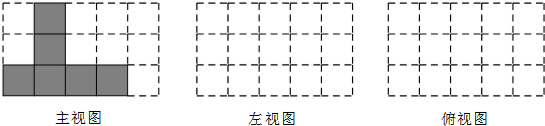
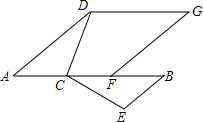（1）该几何体的表面积（含下底面）为
 
；
（2）该几何体的主视图如图所示，请在下面方格纸中分别画出它的左视图和俯视图．
如图，点C在线段AB上，AD∥EB，AC=BE，∠ADC=∠BCE．
（1）求证：△ACD≌△BEC；
（2）点F在线段AB上，若FG∥AD且FG=BC，连接DG．猜想四边形ADGF是怎样特殊的四边形，并给出证明．
计算：20140+
8
-4sin45°-(
1
2
)-2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网