题目内容
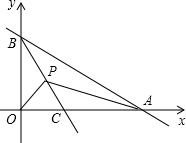 如图,A、B分别为x轴和y轴正半轴上的点.OA、OB的长分别是x2-14x+48=0的两根(OA>OB),直线BC平分∠ABO交x轴于C点,P为BC上一动点,P点以每秒1个单位的速度从B点开始沿BC方向向终点C移动
如图,A、B分别为x轴和y轴正半轴上的点.OA、OB的长分别是x2-14x+48=0的两根(OA>OB),直线BC平分∠ABO交x轴于C点,P为BC上一动点,P点以每秒1个单位的速度从B点开始沿BC方向向终点C移动(1)设△APB和△OPB的面积为S1,S2,则S1:S2=
(2)P点移动时间为t,当t=
考点:勾股定理,坐标与图形性质,角平分线的性质,等腰三角形的判定
专题:
分析:(1)过P点作PD⊥BO,PH⊥AB,垂足分别为D、H,由BC为∠ABO的平分线,可得PH=PD,则可得S1:S2=AB:OB,又∵OA、OB的长是方程x2-14x+48=0的两根(OA>OB),解方程即可求得OA,OB的长,则可得S1:S2的值;
(2)分别取三个点做顶角的顶点,然后求出符合题意的t的值.
(2)分别取三个点做顶角的顶点,然后求出符合题意的t的值.
解答: 解:(1)如图,过P点作PD⊥BO,PH⊥AB,垂足分别为D、H,
解:(1)如图,过P点作PD⊥BO,PH⊥AB,垂足分别为D、H,
∵BC为∠ABO的平分线,
∴PH=PD,
∴S1:S2=AB:OB,
又∵OA、OB的长是方程x2-14x+48=0的两根(OA>OB),
解方程得:x1=8,x2=6,
∴OA=8,OB=6,
∴AB=10,
∴S1:S2=AB:OB=5:3;
(2)①OP=OC时,t=
;
②PC=PO时,P在OC的中垂线上,xp=1.5,代入直线BC的解析式y=-2x+6,
得P(1.5,3),
利用勾股定理可得PC=
=
,
PB=BC-PC=3
-
=
,
所以t=
;
③CP=CO=3时,t=3
-3.
故答案为5:3;
秒或
秒或(3
-3)秒.
 解:(1)如图,过P点作PD⊥BO,PH⊥AB,垂足分别为D、H,
解:(1)如图,过P点作PD⊥BO,PH⊥AB,垂足分别为D、H,∵BC为∠ABO的平分线,
∴PH=PD,
∴S1:S2=AB:OB,
又∵OA、OB的长是方程x2-14x+48=0的两根(OA>OB),
解方程得:x1=8,x2=6,
∴OA=8,OB=6,
∴AB=10,
∴S1:S2=AB:OB=5:3;
(2)①OP=OC时,t=
9
| ||
| 5 |
②PC=PO时,P在OC的中垂线上,xp=1.5,代入直线BC的解析式y=-2x+6,
得P(1.5,3),
利用勾股定理可得PC=
| 1.52+32 |
3
| ||
| 2 |
PB=BC-PC=3
| 5 |
3
| ||
| 2 |
3
| ||
| 2 |
所以t=
3
| ||
| 2 |
③CP=CO=3时,t=3
| 5 |
故答案为5:3;
9
| ||
| 5 |
3
| ||
| 2 |
| 5 |
点评:本题主要考查了三角形的面积,勾股定理,一元二次方程的应用,等腰三角形的判定,有一定难度.分类讨论是解题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
下列命题中,真命题是( )
| A、对角线相等的四边形是矩形 |
| B、四个角相等的四边形是矩形 |
| C、对角线互相垂直的四边形是菱形 |
| D、对角线互相垂直且平分的四边形是正方形 |
抛物线y=x2-4x+5的顶点坐标是( )
| A、(2,1) |
| B、(-2,1) |
| C、(2,5) |
| D、(-2,5) |
 如图,已知△OAB的顶点为A(-6,0),B(0,2),O是坐标原点,将△OAB绕点O按顺时针旋转90°,得到△ODC.
如图,已知△OAB的顶点为A(-6,0),B(0,2),O是坐标原点,将△OAB绕点O按顺时针旋转90°,得到△ODC.