题目内容
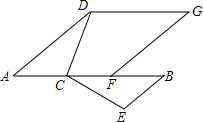 如图,点C在线段AB上,AD∥EB,AC=BE,∠ADC=∠BCE.
如图,点C在线段AB上,AD∥EB,AC=BE,∠ADC=∠BCE.(1)求证:△ACD≌△BEC;
(2)点F在线段AB上,若FG∥AD且FG=BC,连接DG.猜想四边形ADGF是怎样特殊的四边形,并给出证明.
考点:全等三角形的判定与性质,平行四边形的判定
专题:
分析:(1)根据平行线的性质,可得内错角相等,根据AAS,可得两三角形全等;
(2)根据全等三角形的性质,可得对应边相等,根据等量代换,可得AD与FG的关系,根据平行四边形的判定,可得证明的结论.
(2)根据全等三角形的性质,可得对应边相等,根据等量代换,可得AD与FG的关系,根据平行四边形的判定,可得证明的结论.
解答:(1)证明:∵AD∥EB,
∴∠A=∠B.
在△ACD和△BEC中,
∴△ACD≌△BEC(AAS);
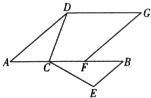
(2)猜想:四边形ADGF是平行四边形.
证明:∵△ACD≌△BEC,
∴AD=CB.
∵FG=BC,
∴AD=FG.
∵FG∥AD,
∴四边形ADGF是平行四边形.
∴∠A=∠B.
在△ACD和△BEC中,
|
∴△ACD≌△BEC(AAS);

(2)猜想:四边形ADGF是平行四边形.
证明:∵△ACD≌△BEC,
∴AD=CB.
∵FG=BC,
∴AD=FG.
∵FG∥AD,
∴四边形ADGF是平行四边形.
点评:本题考查了全等三角形的判定与性质,(1)利用AAS是判定三角形全等,(2)利用一组对边平行且相等的四边形是平行四边证明结论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列命题中,真命题是( )
| A、对角线相等的四边形是矩形 |
| B、四个角相等的四边形是矩形 |
| C、对角线互相垂直的四边形是菱形 |
| D、对角线互相垂直且平分的四边形是正方形 |
抛物线y=x2-4x+5的顶点坐标是( )
| A、(2,1) |
| B、(-2,1) |
| C、(2,5) |
| D、(-2,5) |
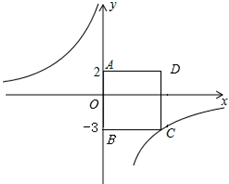 如图,四边形ABCD为正方形.点A的坐标为(0,2),点B的坐标为(0,-3),反比例函数
如图,四边形ABCD为正方形.点A的坐标为(0,2),点B的坐标为(0,-3),反比例函数 解不等式组:
解不等式组: