题目内容
8．
如图，已知△ABC的面积是15平方厘米，BD：DC=AD：ED=2：1，求阴影部分的面积．
分析 连接DF，由AD：ED=2：1，得到AE=DE，于是得到△ABE=S△BDE，S△AEF=S△DEF，由BD：DC=2：1，于是得到S△BDF=2S△CDF，因此S△ABF=S△BDF，于是得到S△CDF=$\frac{1}{5}$S△ABC，即可得到S阴影=S△BDF=2S△CDF．
解答 
解：连接DF，
∵AD：ED=2：1，
∴AE=DE，
∴S△ABE=S△BDE，S△AEF=S△EFD，
∵BD：DC=2：1，
∴S△BDF=2S△CDF，
∴S△ABF=S△BDF=2S△CDF，
∴S△CDF=$\frac{1}{5}$S△ABC=15×$\frac{1}{5}$=3，
∴S阴影=S△BDF=2S△CDF=6．
点评 本题考查了三角形的面积，解题的关键是连接DF，根据等高三角形的面积和底的正比关系进行计算．
练习册系列答案
名校联盟快乐课堂系列答案
黄冈创优卷系列答案
相关题目
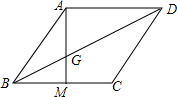如图，四边形ABCD为菱形，M为BC上一点，连接AM交对角线BD于点G，并且∠ABM=2∠BAM．
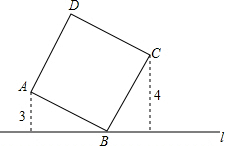如图，直线l过正方形ABCD的顶点B，点A、点C到直线l的距离分别是3和4，则该正方形中AC的长是5$\sqrt{2}$．
如图，点B、C在线段AD上，AC=DB，AF∥DE，AF=DE，求证：△ABF≌△DCE．
已知，如图长方形ABCD中，AB=3cm，AD=9cm，将此长方形折叠，使点B与点D重合，折痕为EF，求BE的长．