题目内容
13.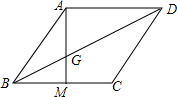 如图,四边形ABCD为菱形,M为BC上一点,连接AM交对角线BD于点G,并且∠ABM=2∠BAM.
如图,四边形ABCD为菱形,M为BC上一点,连接AM交对角线BD于点G,并且∠ABM=2∠BAM.(1)求证:AG=BG;
(2)若点M为BC的中点,同时S△BMG=1,求三角形ADG的面积.
分析 (1)根据菱形的对角线平分一组对角,得出∠ABD=∠CBD,再根据∠ABM=2∠BAM,得出∠ABD=∠BAM,然后根据等角对等边证明即可.
(2)根据相似三角形面积的比等于相似比的平方即可求得.
解答 (1)证明:∵四边形ABCD是菱形,
∴∠ABD=∠CBD,
∵∠ABM=2∠BAM,
∴∠ABD=∠BAM,
∴AG=BG;
(2)解:∵AD∥BC,
∴△ADG∽△MBG,
∴$\frac{AG}{GM}$=$\frac{AD}{BM}$,
∵点M为BC的中点,
∴$\frac{AD}{BM}$=2,
∴$\frac{{S}_{△ADG}}{{S}_{△BMG}}$=($\frac{AD}{BM}$)2=4
∵S△BMG=1,
∴S△ADG=4.
点评 本题考查了菱形的性质,等腰三角形的判定,三角形相似的判定和性质,熟练掌握性质定理是解题的关键.

练习册系列答案
相关题目
8.在同一坐标系中,作y=2x2、y=-2x2、y=0.5x2的图象,它们共同特点是( )
| A. | 都是关于x轴对称,抛物线开口向上 | B. | 都是关于原点对称,顶点都是原点 | ||
| C. | 都是关于y轴对称,抛物线开口向下 | D. | 都是关于y轴对称,顶点都是原点 |
10.a是最大的负整数,b是绝对值最小的有理数,在a2011+$\frac{{b}^{2013}}{2012}$=( )
| A. | -1 | B. | 0 | C. | $\frac{1}{2012}$ | D. | 2011 |
 如图,已知△ABC的面积是15平方厘米,BD:DC=AD:ED=2:1,求阴影部分的面积.
如图,已知△ABC的面积是15平方厘米,BD:DC=AD:ED=2:1,求阴影部分的面积.