题目内容
10. 如图,将矩形纸ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E,若CD=6,AD=18,则BE=10.
如图,将矩形纸ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E,若CD=6,AD=18,则BE=10.
分析 先证明BE=DE,设BE=DE=x,在RT△DEC中,利用勾股定理即可解决.
解答  解:∵四边形ABCD是矩形,
解:∵四边形ABCD是矩形,
∴AD=BC=18,AD∥BC,∠C=90°,
∴∠ADB=∠DBC,
∵△BDF是由△BDA翻折得到,
∴∠ADB=∠BDF,
∴∠EDB=∠EBD,
∴BE=ED,设BE=ED=x,
在RT△EDC中,∵∠C=90°,CD=6,DE=x,EC=18-x,
∴x2=62+(18-x)2,
∴x=10,
∴BE=10.
故答案为10.
点评 本题考查翻折变换、矩形的性质、勾股定理等知识,解题的关键是利用勾股定理,构建方程,把问题转化为方程解决,属于中考常考题型.

练习册系列答案
相关题目
19.掷两个骰子点数的和为偶数,这一事件为( )
| A. | 必然事件 | B. | 不确定事件 | C. | 不可能事件 | D. | 随机事件 |
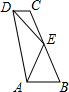 已知:如图,AB∥CD,AE平分∠BAD交BC于E,BE=CE.求证:AD=AB+CD.
已知:如图,AB∥CD,AE平分∠BAD交BC于E,BE=CE.求证:AD=AB+CD. 如图所示的正方形内,∠1,∠2都是15°.求证:黄色三角形是等边三角形.
如图所示的正方形内,∠1,∠2都是15°.求证:黄色三角形是等边三角形.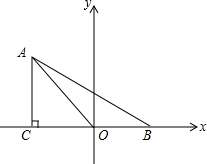 如图,在平面直角坐标系中,已知点A(xA,2)在第二象限,AC⊥x轴于点C,△AOC的面积为$\sqrt{3}$,点B的坐标为($\sqrt{3}$,0).
如图,在平面直角坐标系中,已知点A(xA,2)在第二象限,AC⊥x轴于点C,△AOC的面积为$\sqrt{3}$,点B的坐标为($\sqrt{3}$,0).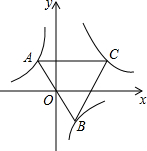 如图,已知点A是双曲线y=-$\frac{5}{x}$在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第一象限内,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$(k>0)上运动,则k的值是15.
如图,已知点A是双曲线y=-$\frac{5}{x}$在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第一象限内,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$(k>0)上运动,则k的值是15.