题目内容
7.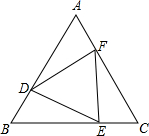 如图,D、E、F分别是等边△ABC各边上的点,且BD=CE=2,BE=CF.
如图,D、E、F分别是等边△ABC各边上的点,且BD=CE=2,BE=CF.(1)求证:△DEF是等边三角形;
(2)若∠DEC=150°,求等边△ABC的周长.
分析 (1)由等边三角形的性质易得AB=BC=AC,∠A=∠B=∠C=60°,由已知易得BD=CE=AF,AD=BE=CF,可得△BDE≌△CEF≌△AFD,由全等三角形的性质可得DE=FD=EF,证得结论;
(2)首先由∠DEC=150°,易得∠FEC=90°,可得△ADF、△BED、△CFE均为直角三角形,可得∠CFE=∠ADF=∠BDE=30°,由直角三角形的性质可得CF=AD=BE=2BD=4,可得AB,易得结果.
解答 (1)证明:∵△ABC是等边三角形,
∴AB=BC=AC,∠A=∠B=∠C=60°,
∵BD=CE,BE=CF,
∴BD=CE,BE=CF,
∴BD=CE=AF,AD=BE=CF,
在△BDE与△CEF中,
$\left\{\begin{array}{l}{BD=CE}\\{∠B=∠C}\\{BE=CF}\end{array}\right.$,
∴△BDE≌△CEF(SAS),
∴DE=EF,
同理可得△BDE≌△AFD,
∴DE=FD,
∴DE=FD=EF,
∴△DEF为等边三角形;
(2)解:∵∠DEC=150°,∠DEF=60°,
∴∠FEC=90°,
∴△ADF、△BED、△CFE均为直角三角形,且∠CFE=∠ADF=∠BDE=30°,
∵BD=CE=2,
∴CF=AD=BE=2BD=4,
∴AB=BC=AC=6,
∴等边△ABC的周长为:6×3=18.
点评 本题主要考查了等边三角形的性质及判定和全等三角形的性质及判定,综合利用各定理是解答此题的关键.

练习册系列答案
相关题目
18.在-4,-3,-2,-1,0,1,2这些整数中,能使不等式4-x≥6成立的有( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
19.掷两个骰子点数的和为偶数,这一事件为( )
| A. | 必然事件 | B. | 不确定事件 | C. | 不可能事件 | D. | 随机事件 |
16.下面各图象不能表示y是x的函数的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图所示的正方形内,∠1,∠2都是15°.求证:黄色三角形是等边三角形.
如图所示的正方形内,∠1,∠2都是15°.求证:黄色三角形是等边三角形.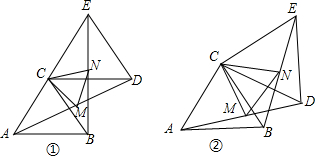
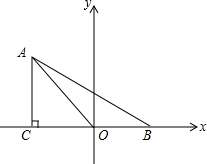 如图,在平面直角坐标系中,已知点A(xA,2)在第二象限,AC⊥x轴于点C,△AOC的面积为$\sqrt{3}$,点B的坐标为($\sqrt{3}$,0).
如图,在平面直角坐标系中,已知点A(xA,2)在第二象限,AC⊥x轴于点C,△AOC的面积为$\sqrt{3}$,点B的坐标为($\sqrt{3}$,0).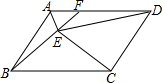 在图中,ABCD是平行四边形,F在AD上,△AEF的面积=8cm2,△DEF的面积=12cm2,四边形BCDF的面积=72cm2,求出△CDE的面积.
在图中,ABCD是平行四边形,F在AD上,△AEF的面积=8cm2,△DEF的面积=12cm2,四边形BCDF的面积=72cm2,求出△CDE的面积.