题目内容

15．点A、B、C为⊙O上的三点，如果∠AOB=70°，则∠ACB=35°或145°．

分析 分类讨论：当点C在优弧AB上，根据圆周角定理直接得到∠ACB=35°；当点C在弧AB上，根据圆内接四边形的性质易得∠ACB=145°．

解答 解：当点C在优弧AB上，则∠ACB=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×70°=35°；
当点C在弧AB上，则∠ACB=180°-35°=145°，
所以∠ACB=35°或145°．
故答案为35°或145°．

点评 本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．

练习册系列答案
相关题目
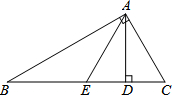10．如图，在△ABC中，∠BAC=90°，∠B=30°，AD⊥BC，AE平分∠BAD，则△ABC∽△DBA，△BAD∽△ACD（写出一个三角形即可）．
11．-$\frac{1}{3}$的相反数是（　　）
A．3B．$\frac{1}{3}$C．-3D．-$\frac{1}{3}$
3．（1）如图（1）在△ABC中，点D、E、Q分别在AB、AC、BC上，且DE∥BC，AQ交DE于点P，求证：$\frac{DP}{BQ}=\frac{PF}{QC}$．
（2）如图（2）在△ABC中，∠BAC=90°，AB=AC=1，正方形DEFG的四个顶点在△ABC的边上，连接AG、AF分别交DE于M、N两点，求MN的长．
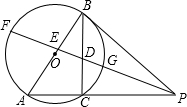10．已知：如图AB是⊙O的直径，PB切⊙O于点B，PA交⊙O于点C，PF分别交AB、BC于E、D，交⊙O于F、G，且BE、BD恰好是关于x的方程x2-6x+（m2+4m+13）=0（其中m为实数）的两根．
（1）求证：△PBC∽△BAC；
（2）求证：PF平分∠APB；
（3）若GE•EF=6$\sqrt{3}$，求∠PBC的度数．
20．若x，y为实数，且|x-2|+$\sqrt{y+3}$=0，则（x+y）2015的值为-1．
7．阅读材料：
关于x的方程：
x+$\frac{1}{x}=c+\frac{1}{c}$的解为：x1=c，x2=$\frac{1}{c}$
x-$\frac{1}{x}=c-\frac{1}{c}$（可变形为x+$\frac{-1}{x}=c+\frac{-1}{c}$）的解为：x1=c，x2=$\frac{-1}{c}$
x+$\frac{2}{x}=c+\frac{2}{c}$的解为：x1=c，x2=$\frac{2}{c}$
x+$\frac{3}{x}=x+\frac{3}{c}$的解为：x1=c，x2=$\frac{3}{c}$
…
根据以上材料解答下列问题：
（1）①方程x+$\frac{1}{x}=2+\frac{1}{2}$的解为${x}_{1}=2，{x}_{2}=\frac{1}{2}$
②方程x-1+$\frac{1}{x-1}$=2+$\frac{1}{2}$的解为${x}_{1}=3，{x}_{2}=\frac{3}{2}$
（2）解关于x方程：x-$\frac{3}{x-2}=a-\frac{3}{a-2}$（a≠2）
4．下列运算正确的是（　　）
A．（-2x2）3=-8x6B．（a3）2=a5C．a3•（-a）2=-a5D．（-x）2÷x=-x
5．已知x（x-2）=8，求代数式（x-2）2+2x（x-1）-5的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网