题目内容
1.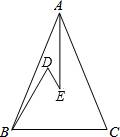 如图,在△ABC中,AB=AC,D、E是△ABC内的两点,AE平分∠BAC,∠D=∠DBC=60°,若BD=5cm,DE=3cm,则BC的长是8cm.
如图,在△ABC中,AB=AC,D、E是△ABC内的两点,AE平分∠BAC,∠D=∠DBC=60°,若BD=5cm,DE=3cm,则BC的长是8cm.
分析 作出辅助线后根据等边三角形的判定得出△BDM为等边三角形,△EFD为等边三角形,从而得出BN的长,进而求出答案.
解答  解:延长DE交BC于M,延长AE交BC于N,
解:延长DE交BC于M,延长AE交BC于N,
∵AB=AC,AE平分∠BAC,
∴AN⊥BC,BN=CN,
∵∠DBC=∠D=60°,
∴△BDM为等边三角形,
∴BD=DM=BM=5,
∵DE=3,
∴EM=2,
∵△BDM为等边三角形,
∴∠DMB=60°,
∵AN⊥BC,
∴∠ENM=90°,
∴∠NEM=30°,
∴NM=1,
∴BN=4,
∴BC=2BN=8(cm),
故答案为8.
点评 此题主要考查了等腰三角形的性质和等边三角形的性质,能求出MN的长是解决问题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
9.下列交通标志既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
6.已知-1是关于x的方程x2+4x-m=0的一个根,则这个方程的另一个根是( )
| A. | -3 | B. | -2 | C. | -1 | D. | 3 |
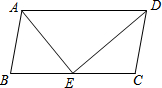 如图,在?ABCD中,DE是∠ADC的平分线,交BC于点E.
如图,在?ABCD中,DE是∠ADC的平分线,交BC于点E.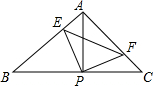 如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③2S四边形AEPF=S△ABC;④BE+CF=EF.上述结论中始终正确的有( )
如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③2S四边形AEPF=S△ABC;④BE+CF=EF.上述结论中始终正确的有( )