题目内容
5.有6张正面分别写有数字-4,-2,0,2,3,4的卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为k,则使关于x为自变量的一次函数y=kx+k-2经过第二象限,且关于x的分式方程$\frac{k}{x-2}$-2=$\frac{2}{2-x}$有整数解的概率是$\frac{1}{3}$.分析 先求出方程的解,再找出使分式方程有整数解的数,最后根据概率公式进行计算即可.
解答 解:∵方程$\frac{k}{x-2}$-2=$\frac{2}{2-x}$的解是x=$\frac{6+k}{2}$,
∴-4,-2,0,2,4能使方程有整数解,当k=-2时,方程有增根,
又直线y=kx+k-2经过第二象限,则k只能取-4,4;
则符合题意的概率为:$\frac{2}{6}$=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 此题考查了概率公式;用到的知识点为:概率=所求情况数与总情况数之比,得到使分式方程有整数解的情况数是解决本题的关键.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
16.已知点A是反比例函数xy=-6图象上的一点.若AB垂直于y轴,垂足为B,则△AOB的面积是( )
| A. | 3 | B. | -3 | C. | 6 | D. | -6 |
13.10名同学分成甲、乙两队进行篮球比赛,他们的身高(单位:cm)如下表所示:
设两队队员身高的平均数依次为$\overline{x}$甲,$\overline{x}$乙,身高的方差依次为S2甲,S2乙,则下列关系中正确的是( )
| 队员1 | 队员2 | 队员3 | 队员4 | 队员5 | |
| 甲队 | 177 | 176 | 175 | 172 | 175 |
| 乙队 | 170 | 175 | 173 | 174 | 183 |
| A. | $\overline{x}$甲=$\overline{x}$乙,S2甲>S2乙 | B. | $\overline{x}$甲<$\overline{x}$乙,S2甲<S2乙 | ||
| C. | $\overline{x}$甲>$\overline{x}$乙,S2甲>S2乙 | D. | $\overline{x}$甲=$\overline{x}$乙,S2甲<S2乙 |
14.将抛物线y=3x2向上平移3个单位,然后再向左平移2个单位所得抛物线的解析式是( )
| A. | y=3x2+12x+15 | B. | y=3x2-12x+15 | C. | y=3x2+12x+9 | D. | y=3x2-12x+9 |
15.不等式(a-2012)x>a-2012的解集是x<1.则a应满足的条件是( )
| A. | a=2012 | B. | a<2012 | C. | a>2012 | D. | 无法确定 |
 已知:在四边形ABCD中,M是边BC的中点,AM、BD互相平分并交于点O,求证:四边形AMCD是平行四边形.
已知:在四边形ABCD中,M是边BC的中点,AM、BD互相平分并交于点O,求证:四边形AMCD是平行四边形.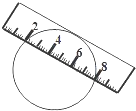 如图,一宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm),则该圆的半径为$\frac{13}{4}$cm.
如图,一宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm),则该圆的半径为$\frac{13}{4}$cm.